척척학사의 공부노트입니다!
틀린 부분이 굉장히 많을 수 있으며
오류의 정정 및 조언을 해주신다면 정말 감사하겠습니다!
6주차 강의 정리 및 번역 내용입니다
1. Basic Bipolar Junction Transistor in forward active mode
1) Formation of a Bipolar Junction Transistor(BJT)
전자회로 중에서 가장 중요한 요소가 스위치와 정류기이다. 이 두 소자는 PN 접합의 기본적인 구조를 확장시킴으로써 구현이 가능하다. PN 구조의 에너지 밴드를 고려해보자. P 영역에서 N 영역의 전자를 방해는 장벽을 형성된다. 이와 반대로 N 영역에서는 P 영역의 정공을 방해하는 장벽을 형성한다.
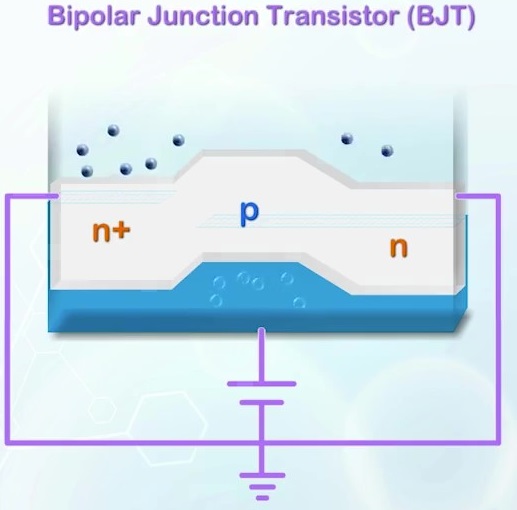
만약 P 영역의 반대편에 또다른 N 영역을 추가한다면 서로 장벽으로 분리된 채 수많은 자유 전자를 보유한 N 영역 두개를 얻을 수 있다. 순방향 전압에 의해 P 영역의 장벽이 낮아진다, 장벽을 통과해 넘어갈 수 있는 전자의 수가 지수 함수적으로 증가하게 된다. 이를 통해 각각의 영역에서 한 개씩, 총 3개의 터미널로 구성된 소자를 만들게 된다. 이를 Bipolar Junction Transistor, BJT라고 부른다.

기본적으로 한 개의 P 영역과 두개의 N 영역으로 이루어진 구조를 NPN 형이라 부르며 그 상징은 위와 같다. 그 중 가운데, 전류의 흐름을 조절하는 부분을 베이스(base)라고 부른다. 양 방향으로 전류의 흐름이 가능하게 하기 위해서 두 N 영역에는 다른 전압이 인가된다. 그 중 전자가 베이스로 주입되는 N 영역을 이미터(emitter), 베이스로부터 전자가 주입되는 N 영역을 콜렉터(collector)라고 부른다. 이미터는 콜렉터보다 더 높은 도핑을 요구한다. 자세한 이유는 뒤에서 다루도록 하자.

이러한 NPN 구조 외에도 N이 양 P에 연결되어 있는 PNP형도 존재하며 정공을 캐리어로써 활용한다. 이에 상응하는 상징은 위와 같다. 두 구조의 심볼에서 화살표의 방향은 베이스와 이미터 사이의 전류의 방향을 나타낸다.

BJT의 동작을 이해하기 위해서 이전에 했던 것처럼 열평형상태 소자의 정전기적 특성부터 살펴보자. 설명은 NPN을 기준으로 진행될 예정이며 PNP는 전압의 극성과 영향을 주는 캐리어만 바꿔준다면 똑같은 원리로 이해할 수 있다. NPN 트렌지스터는 두개의 PN 접합으로 이루어졌다. 이전에 배웠던 내용을 기반으로 전하의 분포는 위 그래프와 같다. 전하를 적분함으로써 실리콘의 유전율로 나눠진 전기장을 얻을 수 있다. 이를 다시 적분함으로써 포텐셜을 구한다. 이를 통해 에너지 밴드를 구하게 된다.

최종적으로 이에 상응하는 세 영역의 minority 캐리어 농도도 그래프로 편할 수 있다. 각 영역의 minority 캐리어는 이전에 배웠던 내용과 동일하다. 이러한 도핑 농도는 일반적으로 이미터가 가장 농도가 높고 콜렉터의 농도가 가장 낮다. 그리고 평형 상태의 minority 캐리어 농도가 이미터에서 콜렉터 방향으로 점점 증가한다.
2) Basic operation principles in the forward active mode
BJT를 동작시키기 위해, 세 터미널에 서로 다른 전압을 인가한다. 이 전압은 순방향일수도 역방향일수도 있다. 그리고 2개의 PN 접합이 존재하기 때문에, 가능한 경우의 수는 총 4가지다. 이 중 가장 중요한 상황은 베이스-이미터 사이의 순방향 전압, 베이스-콜렉터 사이의 역방향 전압이다. 이를 forward active operation region이라고 부른다. 이것이 회로에 BJT를 연결했을 때 가장 흔하게 사용되는 예로 베이스의 전압이 콜렉터와 이미터 사이의 전류 흐름을 조절하게 된다.

이 동작 상황의 에너지 밴드를 살펴보자. 먼저 열평형상태에서의 에너지 밴드로부터 시작한 뒤, 같은 양 전압을 베이스와 콜렉터에 인가한다. 그리고 이미터는 접지 시킨다. 이후 베이스-콜렉터를 역방향전압으로 만들기 위해 더욱 큰 양전압을 콜렉터에 인가시킨다면, 다음과 같은 에너지 밴드를 구할 수 있다. 위 상황에서 이미터에서 콜렉터로 이동할 수 있는 전자의 양이 베이스-이미터 사이의 전압에 의해 조절된다.

다음은 minority 캐리어 농도에 대해 살펴보자. 역시나 열평형상태에서 베이스-이미터 접합에 순방향 전압을 인가하자. 이를 통해, 베이스-이미터 사이 공핍 영역에 캐리어 수가 증가하게 된다. 반면에 베이스-콜렉터 사이 공핍 영역에서는 역방향 전압에 의해 캐리어의 수가 줄어들게 된다. 일반적인 BJT 구조에서 베이스의 두께는 굉장히 얇다. 그렇기 때문에 short-diode 캐리어 농도를 기반으로 양 끝단을 직선으로 이음으로써 농도 분포를 표현한다.

BJT의 forward active 모드의 일반적인 개념에 대해 더 알아보자. BJT가 스위치로써 작동한 다는 것을 기억해 두자. 이상적으로 베이스-이미터 사이에 순방향 전압을 유도하기 위해 베이스에 양전압을 인가시키는 경우, 이미터의 모든 전자들이 콜렉터로 이동하고 베이스로 누설되지 않아야한다. 이는 마치 수도꼭지를 킨 경우 모든 물이 흘러야지, 수도꼭지로 세 나가는 것을 원치 않는 것과 같다. 하지만 베이스가 또 다른 PN 접합을 형성하기 때문에 불가능하며 몇몇 전류는 무조건 베이스를 통해 흘러나가게 된다.

베이스 전류와 콜렉터 전류 모두 이미터로부터 흐르며 이 중 이미터로 흐르는 전류의 크기를 최대로 늘리는 것이 목표다. 기하학을 기반으로 베이스 장벽을 작게하고 콜렉터의 장벽을 크게 한 뒤 베이스 컨택에 샛길을 둠으로써 이룰 수 있으며, 전자의 운동량 또한 콜렉터로 전자가 흐르게 영향을 준다.

또 다른 중요한 관점은 콜렉터의 전압을 독립시킴으로써 베이스의 전압에 영향을 주지 않게 하는 것이다. 역방향 전압의 베이스-콜렉터 접합이 이 목적에 해당하며, 어떠한 전압이라도 콜렉터에 인가된다면 베이스 전압을 변화시키는 대신에 베이스-콜렉터 사이 공핍 영역을 줄어들게 한다. 이를 통해 콜렉터는 도달하는 전자를 수동적으로 얻게 되고 베이스-콜렉터 사이의 공핍 영역에 존재하는 전기장을 통해 이동시킨다.
이것이 기본적인 BJT의 작동 원리이다. 작은 베이스 전류로 큰 콜렉터 전류를 얻을 수 있기 때문에, BJT는 또한 증폭기로써 활용할 수 있다. 이는 마치 파이프에서 물의 흐름을 조절하기 위해 몇방울의 물을 활용하는 것과 같다고 볼 수 있다.
3) Current components in the forward active mode

BJT의 forward active 모드의 기본적인 작동 원리에 대해 알아봤다. 이번에는 캐리어의 구체적인 움직임에 대해 알아보자. BJT의 전체 구동은 베이스-이미터 접합에 의해 제어되며 이는 이전에 배운 PN 접합과 같다. 베이스-이미터 접합에 순방향 전압이 걸린다면, 전자와 정공에 의한 전류를 트랜지스터에서 서로 다른 위치에서 측정 가능하다. 이미터에선 확산에 의한 정공 전류를 I_Ep로 표시한다. 이 중 “E”는 이미터를 의미하며, “p”는 정공에 의한 전류라는 것을 의미한다. 이와 동시에 majority 캐리어인 전자에 의한 전류 I_En도 존재한다. 이는 베이스 전자를 이동하게 한다.

베이스 영역에서는, 이미터의 정공 전류를 공급하는 majority 캐리어인 정공에 의한 전류가 발생한다. 이를 I_Bp1라고 부른다. I_Bp1와 I_Ep는 같은 전류이지만 서로 다른 지역에서 측정했기 때문에 다른 이름으로 부른다.

이미터에서 베이스로 들어온 대부분의 전자는 콜렉터로 이동한다. 이들을 I_Cn이라고 표현한다. 몇몇 전자들은 콜렉터에 도달하지 못하고 베이스에서 정공과 재결합된다. 비록 정공에서 재결합되는 전자의 수가 굉장히 적을지여도 이를 무시할 수는 없다. 이 재결합이 베이스에서 재결합된 정공을 다시 채우기 위해 여분의 정공에 의한 전류를 발생하고 I_Bp2가 이에 해당한다. 그리고 아직 베이스-콜렉터 간 역방향 전압이 남아있지만 이는 굉장히 작기 때문에 무시할 수 있다.

이렇게 전류의 요소들이 구체화 된 뒤, 이를 통해 몇몇 파라미터를 통한 성능을 정의할 수 있다. 먼저 이미터의 주입 효율(injection efficiency)이며 이는 감마로 표현된다. 이는 전체 전류 중 유효 전류로 측정할 수 있다. 이미터 전류 중 I_En은 콜렉터의 전류에 기여하는 아주 유용한 요소이다. I_Ep는 베이스의 누설 전류 I_Bp1의 일부분이다. 따라서 감마는 I_En / (I_Ep + I_En)로 정의한다. 이상적으로 감마는 1이 되어야 하지만 현실적으로 0.999가 가능한 값이다.

두번째 파라미터는 베이스의 전달 함수 (transport factor) alpha_T이다. 이는 이미터에서 주입된 전자 중 콜렉터에 도달하는 양으로 측정한다. 현실에서는 몇몇 전자들이 정공과 재결합하여 I_Bp2를 형성하고 콜렉터에 도달하는 대신 누설되게 된다. 따라서 alpha_T는 I_Cn / I_En으로 정의된다. 이 또한 이상적으로는 1이지만 현실적으로 0.99까지 가능하다.

가장 많이 인용되는 BJT 파라미터는 전류 게인(current gain) alpha이다. 이는 콜렉터의 전류와 이미터의 전류 비로 측정 가능하며 베이스의 전압은 접지되어 있다. 수학적으로 이는 I_C / I_E 혹은 I_Cn / ( I_En + I_Ep)로 표현한다. 이는 곧 alpha는 감마 * alpha_T와 같다는 것을 알 수 있다. 이상적으론 누설전류가 발생하지 않기에 1이 되어야 한다. 하지만 현실적으론 0.99 정도의 값을 보이며 주로 alpha_T에 의해 제한을 받는다.

마지막 파라미터는 이미터의 전류 게인 베타이다. 이는 콜렉터 전류와 베이스 전류의 비로 측정할 수 있다. 수학 적으론 I_C / I_B 혹은 I_Cn / ( I_Bp1 + I_Bp2)로 정의한다. 이는 곧 alpha / ( 1 – alpha)와 같다. 이상적으론 베타가 I_B가 0이기 때문에 무한대가 되어야 하지만, 현실적으론 100~200의 값을 가진다.
4) Current-voltage characteristics in the forward active mode
BJT의 전류 전압 특성 그래프를 살펴보자. 세 개의 터미널 중 이미터는 일반적으로 접지된다. 그리고 콜렉터와 베이스의 전류를 각각 인가된 전압에 함수로 살펴보아야 한다. 베이스-이미터 접합에서 흐르는 전류는 PN 접합의 전류와 다르지 않다.

이에 해당하는 I_E를 I_E0*[exp(q*V_BE/kT) -1]로 표현할 수 있다. 콜렉터와 베이스 전류는 이미터 전류를 alpha를 기준으로 양분한 것이다. 따라서 두 전류는 V_BE에 지수함수적으로 영향을 받으며 위와 같이 주어진 공식을 통해 같은 그래프에 표현할 수 있다. 두 전류의 비는 베타로 표현된다.

지수 함수를 유효하게 살펴보기 위해 로그 스케일로 변환한 그래프를 Gummel plot이라고 부른다. 이는 BJT의 이해에 크게 기여한 Hermann Gummel을 기념하기 위해 명명되었다. 두 선사이의 수직 거리는 전류 게인 베타를 의미하며 전 영역에서 거의 일정하다. V_BE가 작을 때는 공핍 영역의 재결합 전류가 지배적이게 되며 그 수치가 작지만 베이스 전류에 영향을 주게 된다. V_BE가 클 때는 높은 레벨의 주입이 콜렉터의 전류 증가를 느리게 만든다. 이러한 두 영향이 베타를 낮추고 각 전압을 낮추거나 높이게 된다. 만약 베타를 V_BE에 대한 함수로 표현한다면 위와 같은 그래프를 얻는다.

아날로그 회로에서 종종 바이어스 값을 트랜지스터가 원하는 상황에서 작동하기 위해 수정해야 한다. 만약 BJT의 작동 조건 중 하나인 V_BE를 수정하게 된다면 작은 노이즈가 지수 함수이기 때문에 전류의 큰 파동을 유발하게 될 것이다. 그렇기에 안정적인 작동 환경을 구현하기 위해선 회로 구현을 위한 전류 소스를 수정하여 BJT의 전류를 조절한다. 콜렉터 전류를 베타에 대한 함수로 로그 스케일로 표현하면 베타가 콜렉터 전류의 많은 요소의 크기에 의해 일정하다는 것을 알 수 있다.

V_BE에 대한 영향 외에 이번에는 V_CE의 영향에 대해 알아보자. 콜렉터 전압이 베이스-이미터 접합에 분리되어 있기 때문에 이에 콜렉터 전류는 영향을 받지 않는다. 따라서 콜렉터 전류는 V_CE에 비례하지만 굉장히 작을때는 제외해야 한다. 그 이유는 베이스-콜렉터 접합이 역방향전압이 아니기 때문이다. 이에 대해선 아래에서 더 자세히 다루도록 하자. 콜렉터의 전류는 위 이미지와 같이 오직 베이스 전류 혹은 V_BE가 바뀔 때만 변화한다. 콜렉터 전류의 변화는 베이스 전류의 베타 제곱에 비례한다. 만약 V_BE가 전류를 변화시킨다면, 콜렉터의 전류가 지수함수적으로 변화하기 때문에 전류의 간격이 매우 불규칙적이게 될 것이다.
5) Emitter and base design of the BJT

작동 원리에 대해 알아봤으니 이번에는 BJT의 이상적인 성능으로 최적화시키는 디자인을 배워보자. 지금까지 BJT의 기본 원리는 간단하게 이미터 전류 중 콜렉터 전류를 최대화, 베이스 전류를 최소화시키는 것이다. 가장 이상적인 스위치는 I_Bp1와 I_Bp2가 0이 되어야 한다. 이는 감마와 alpha_T를 최대화시키는 것과 같다.

감마는 I_En/ (I_En + I_Ep) 혹은 1/ (1+ I_Ep/ I_En)이다. 즉 감마를 최대화 한다는 것은 I_Ep / I_En를 최소화하는 것이다. 이 둘은 PN 접합에서 전자와 정공의 전류에 상응한다. 이들은 다음과 같은 이상적인 다이오드 공식을 통해서 구할 수 있다.

그리고 이 둘의 비 또한 유도할 수 있다. 일반적으로 이미터와 베이스 영역이 짧기 때문에, 확산 길이가 이미터, 베이스 자체의 길이로 대체할 수 있다. 게다가 루트 n_i를 도핑 농도로 나눈 minority 캐리어 항을 제거할 수 있다. 이에 따른 최종적인 항을 도출한다. 모든 요소들 중 조절할 수 있는 가장 큰 범위를 가진 것은 도핑 농도이다. I_Ep / I_En를 최소화하기 위해서 베이스 도핑보다 이미터의 도핑이 3배 이상으로 디자인 되어야 한다. 이는 정공의 비율을 0.1% 이하로 낮춰 감마가 0.999 정도가 될 수 있게 한다.

Alpha_T의 경우에는 I_Cn / I_En, [1 - (I_Bp2/I_En)]이다. I_En은 PN 접합의 확산 전류이며 베이스 영역에서 전자의 분포 기울기에 해당한다. 이는 q*Dn_B*n_BE/x_B로 정의되며 x_B는 베이스의 중립 영역 두께이다. 공핍 영역이 베이스 넓이에 비교하여 작다고 가정하면, x_B를 W_B라고 볼 수 있다.

재결합 전류 I_Bp2를 측정하기 위해선 베이스의 재결합 주기 tau_B라는 새로운 개념을 알아야 한다. 이는 캐리어가 재결합 전까지 베이스 지역에서 대기하는 평균 시간이다. 이 개념을 통해 재결합 전류를 q * 시간당 재결합되는 캐리어 수로 표현한다. 혹은 수학적으로, q * 베이스에서 minority 캐리어의 전체 수와 같다. 이는 n_B / tau_B다. 만약 평형 캐리어 분포 n_B0가 n_BE와 비교하여 굉장히 작을 때, n_B는 그래프의 삼각형 영역과 같으며 n_BE * W_B / 2이다. 그 결과 재결합 전류는 q*n_BE*W_B/(2*tau_B)가 된다.

I_En과 I_Bp2를 alpha_T에 관한 식에 대입한다면 식이 다음과 같이 정리된다. W_B를 제외한 모든 항들이 일정하거나 조절하기 힘들다. 따라서 베이스의 두께를 줄이는 것이 alpha_T를 높이는 가장 효율적인 방법이다. 이에 0.99까지 값을 얻을 수 있으며, 감마보다 더 높은 트랜지스터 게인을 얻는데 중요하게 역할을 하게 된다. 또한 베이스 영역의 결정 정도도 중요한 요소이다. 그 이유는 재결합을 최소화하여 재결합 주기를 증가시키기 위함이다.
이러한 내용들이 일반적으로 이미터가 베이스보다 더 높은 도핑을 하는 이유이며 동시에 트렌지스터 게인을 최대화하기 위해 베이스를 작게하는 이유이다. 이를 통해 얻을 수 있는 값들은 감마 0.999, alpha_T 0.99, alpha 0.99, beta 100 내외이다.