척척학사의 공부노트입니다!
틀린 부분이 굉장히 많을 수 있으며
오류의 정정 및 조언을 해주신다면 정말 감사하겠습니다!
지난 포스트와 같은 주차 내용입니다.
2021/01/23 - [반도체/edX] - [Semiconductor Devices] PN junction optical properties
[Semiconductor Devices] PN junction optical properties
척척학사의 공부노트입니다! 틀린 부분이 굉장히 많을 수 있으며 오류의 정정 및 조언을 해주신다면 정말 감사하겠습니다! 5주차 내용 정리 및 번역입니다. 5주차. PN junction optical properties and
nagadi.tistory.com
2. Metal-semiconductor contacts
1) 일함수 (Work function)
하나의 물질로 이루어진 재료에서 캐리어의 움직임은 굉장히 간단하다. 하지만, 캐리어는 금속 배선을 통해 서로 다른 소자로 이동한다. 이러한 상황에서 서로 다른 물질인 금속 와이어와 반도체 물질 사이, 금속-반도체 접합의 움직임에 대해 알아야한다. 금속과 반도체는 서로 매우 다른 에너지 밴드 개형을 가지고 있기 때문에 이를 어떻게 그려야 할지 우선적으로 알아보자.

우선적으로 반도체의 에너지 밴드는 전도대, 가전자대, 밴드 갭으로 구성되어 있다. 금속의 에너지 밴드는 페르미 레벨에 해당하는 state에, 전자가 부분적으로 채워진 밴드만 존재한다. 일반적으로 금속의 에너지 밴드를 페르미 레벨을 통해서 표현한다. 페르미 레벨 이 외에 존재하는 state는 대부분 비어있다. 페르미 레벨은 마치 해수면처럼 작용한다. 그렇다면 이 두 물질을 접촉시켰을 때, 에너지 밴드는 어떻게 변화할까? 전자의 에너지가 전기적 포텐셜에 의존하기 때문에, 몇몇 파라미터를 통해 두 시스템의 두 에너지 밴드의 접촉을 정렬할 수 있다.

전자가 진공 혹은 그 어떤 전하에 영향을 받지 않는 공간을 이동할 때, 그들은 전부 같은 전기적 포텐셜을 가지고 있다고 고려할 수 있다. 그리고 이를 포텐셜 에너지가 존재하지 않는다고 볼 수 있다. 하지만 이를 원자핵과 같은 전하를 가진 물체를 주변에 둔다면, 전자는 전기적 포텐셜을 잃고 동일한 양만큼의 음수의 포텐셜 에너지를 가지게 된다.

금속에 있어서 페르미 레벨이 전자가 존재할 수 있는 가장 높은 전기적 포텐셜 에너지이다. 그렇기에 페르미 레벨이 전자를 완전히 자유로운 공간으로 이동하게 하는 에너지의 크기이며 이를 일함수(work-function)라 부른다. 이를 기호로서는 ‘q*phi_M’으로 표현한다. 또한 전자가 다른 원자에 영향을 받지 않고 자유롭게 움직일 수 있는 공간을 일반적으로 진공 레벨 (vacuum level)이라고 부른다. 일함수는 금속의 성질을 나타내기 위한 가장 좋은 특징이다.

반도체 물질은 이런 일함수가 정확하게 고정된 값이 아니며 도핑에 의존한다. 일반적으로 전도대와 진공 레벨의 에너지 차이로 고려한다. 이를 전자 친화도(electron affinity)라고 말하며, Chi라고 표현한다. 실리콘 결정은 이 값이 4.05eV이다. 이를 금속에 대입해 봤을 때, 금속은 밴드 갭이 0 인 반도체라고 고려할 수 있다. 이 경우 일함수와 전자친화도가 거의 같은 의미라고 볼 수 있다.

이렇게 서로 다른 물질이 접촉했을 때, 진공 레벨을 통해 서로 정렬이 된다. 전자는 진공 레벨에서 자유롭게 움직이며 두 물질 사이를 움직일 때 특별한 변화가 전혀 존재하지 않는다. 표면에서 두 물질은 한 물체처럼 서로 섞이게 된다. 이 과정에서 금속의 밴드 갭은 굉장히 단단하고 얇은 평판처럼 고려할 수 있으며 이는 쉽게 휘어지지 않는다. 그리고 반도체의 밴드 갭은 이전에 배웠던 형태와 같이 쉽게 휘어지며 두께가 존재하는 밴드 갭으로 고려한다. 따라서 두 물질이 접촉되게 된다면 반도체의 밴드 갭에 변화가 발생한다. 그리고 서로 다른 형태의 밴드 갭에 따라 굉장히 큰 경계면도 볼 수 있다. 대부분의 전자들이 페르미 레벨 아래에 존재하며, 반도체의 전도대로 이동하기 위해 당연히 충분한 에너지가 필요하다. 이러한 장벽의 크기는 금속-반도체 접합에서 굉장히 중요한 파라미터이다. 이는 쇼트키 장벽이라고 부르며 그 값을 ‘q*phi_B’로 표현한다. 그리고 쇼트키 장벽을 이루는 접합을 쇼트키 다이오드라고 부른다. 쇼트키 다이오드에서는 금속의 전자들이 가전자대로 빈 공간, 정공이 존재할 때만 들어갈 수 있다. 또한 반도체에서 전자로 정공이 움직이는 것도 같은 원리라고 볼 수 있다. 만약 정공이 가전자대로 이동해야 한다면 금속의 페르미 레벨과 가전자대 사이의 장벽을 또한 넘어서야 한다.
2) 쇼트키 접합의 형성

이번에는 금속-반도체 접합의 디테일한 캐리어 움직임에 대해 알아보자. 이를 위해 한 예시를 들자면 금속의 페르미 레벨이 N 타입 실리콘의 밴드갭 중간에 오는 상황을 가정해 보자. 이러한 밴드 구조를 갖춘 뒤의 에너지 밴드가 위와 같다. 그리고 접촉면의 전도대 가장자리의 에너지 레벨을 Ec_M으로 정의한다. 이 예시에서 N형 실리콘의 페르미 레벨의 금속의 에너지 레벨보다 더 높다. 이는 Ec_M 위에서 더 높은 전자 농도를 보인다는 것을 암시한다. 전자는 이에 따라 N형 반도체에서 금속쪽으로 흐를 것이다.

캐리어의 움직임을 더욱 자세히 살펴보기 위해서 물리적으로 어떻게 캐리어가 움직이는지 다시 살펴보자. PN 접합과 비슷하게 Ec_M 보다 더 높은 영역에서 N형 반도체에 전자가 더 많다. 이 전자들은 금속 영역으로 확산에 의해 이동하게 된다. 그리고 금속 영역은 마치 강과 연결된 대양처럼 흘러 들어오는 전자(물)의 양에 크게 영향을 받지 않는다. 그리고 공핌 영역 가정을 활용하여 접합부에 가까운 부분에 공핍 영역이 존재한다고 볼 수 있으며 이는 금속의 캐리어를 끌어들인다. 이는 공핍 영역과 반대 극성을 띄며 표면에 축적되게 되고 결과적으로 전체 시스템은 중성이 된다. 이러한 공핍 영역이 형성된 뒤에는 전자들이 금속면으로 이동하는 것이 이동 방향과 반대되는 전기적인 힘 때문에 더욱 어려워지게 된다. 최종적으로 열 평형 상태에서 공핍 영역 두께가 고정된다. 이제 에너지 밴드에 대해 다시 살펴보자.

열 평형 상태에서 시스템은 쇼트키 다이오드 양 끝에 연결된 0V의 배터리와 연결된 것 같은 외부 전위에 영향을 받는다. PN 접합과 같이 수조 모델에 이를 대입한다면 앞서 설명한 듯이 위와 같은 형태를 얻게 된다. 페르미 레벨이 금속 부의 수면을 의미하는 만큼 이는 외부 전압과 정렬되게 되며, 전자가 전도대에서 금속으로 이동하는 경향의 균형을 맞추기 위해 내부 전위가 발생한다. 이는 마치 P+을 거의 0에 가까운 밴드갭과 많은 수의 캐리어로 가정한다면, P+/N 접합과 유사하다.
3) 열평형상태 쇼트키 접합의 에너지 밴드

PN 접합에서 배웠던 것처럼 캐리어 움직임을 결정하기 위해 에너지 밴드의 개형을 정확히 알아야 한다. 이를 위해 내부 전위와 공핍 영역 두께를 알아야 한다. 내부 전위는 금속과 N형 반도체의 페르미 레벨 차이와 같다. 하지만 금속 영역의 페르미 레벨를 결정(페르미 레벨 정의 참고)하기 위핸 전도대나 가전자대가 없다. 유일한 기준은 진공 레벨이다. 따라서 내부 전위는 금속과 반도체의 일함수 차이로 표현할 수 있으며 그 값은 phi_M - phi_S으로 표현한다. phi_S는 반도체의 일함수이다.

하지만 반도체의 일함수는 고정되어 있지 않으며 도핑 농도에 영향을 받는다. 이러한 일함수는 전자 친화도에 전도대의 가장자리와 페르미 레벨의 차이를 더함으로써 구할 수 있다. 또한 전도대의 가장자리와 페르미 레벨의 차이는 밴드갭의 절반에 해당하는 에너지에 도핑 페르미 레벨 Ef_s와 순수 페르미 레벨 Ei의 차이의 차와 같다. 이는 위의 이미지로 표현되어 있다. 실리콘의 밴드갭과 Ef_s의 Ei의 차이는 도핑 농도를 통해서 구할 수 있는 값이다. 따라서 내부 전위에 해당하는 식을 구할 수 있다. 최종적으로 금속의 일함수와 반도체의 도핑 농도에 대한 식을 구할 수 있다.

공핍 영역 두께를 구하기 위해선 PN 접합에서와 같이 포아송 공식에서부터 시작한다. 금속 반도체 접합에서 전하의 분포는 위 그래프와 같다. 일반적인 PN 접합과 다르게 마치 굉장히 많이 도핑된 P영역처럼, 금속 영역에서는 표면 가까이에 전하들이 모여있기 때문에 이 영역의 공핍 영역을 무시한다. 이후 이전 과정과 같이 전하량를 적분하여 전기장을 구하고 이를 다시 적분하여, 두 영역 사이의 내부 전위를 구할 수 있다. 포아송 공식과 내부 전위에 대한 식을 활용하여 최종적으로 공핍영역의 두께를 구할 수 있으며 이는 PN 접합 중 한 쪽 영역에 공핍 영역이 0과 같다라고 가정한 것과 같은 결과를 보인다.
4) 열평형상태 쇼트키 접합의 캐리어 모션

이번에는 금속-반도체 접합의 전류 요소에 대해 생각해보자. 금속 영역에서는 전류가 측정되는 영역이 하나의 에너지 밴드로 구성되어 있으며 정공과 전자 둘 다 측정이 가능하다. 이는 두 캐리어 모두 저항이 굉장히 작기 때문이다. 반면 반도체 영역에서는 전기전도성을 각각의 가전자대와 전도대에서 측정이 가능하다. N형 반도체를 예시로 정공 농도가 가전자대에서 굉장히 작다. 게다가 저항 또한 크기 때문에 전류가 흐르기에 적절하지 않다. 하지만 전도대에서 N형 도핑에 의해 전자가 굉장히 많다. 그리고 접합에 가까운 얇은 영역을 제외하곤 저항도 낮기 때문에 대부분의 전류가 전자(반도체의 majority carrier)를 이용하여 흐르게 된다. 따라서 금속-반도체 접합을 majority 캐리어를 활용한 소자라고 고려한다. 가끔은 전자나 정공 중 하나의 캐리어만 활용하기 때문에 단극 소자(unipolar device)로 고려한다.

P 영역 실리콘 대신 연결된 금속을 통해서 전도대의 전자에 영향을 주는 높은 저항 영역을 제거할 수 있다. 캐리어가 금소-반도체간 저항을 넘어설만큼 충분한 에너지를 얻는다면 캐리어는 쉽게 금속 영역으로 이동이 가능하다. 높은 저항 영역의 제거는 이러한 전류의 흐름을 더욱 부드럽게 해준다. 하지만 이는 전류를 측정하는 것을 더욱 어렵게 만든다.
PN 접합에서 높은 저항 영역에서 캐리어 수를 측정하는데 확산에 의존한다. (캐리어의 움직임을 제한함으로써)
이러한 높은 저항 영역 없이는 캐리어 수를 측정하는게 많은 양의 캐리어가 흐르고 전도대의 모든 위치에서 매우 빠르기 때문에 이전보다 훨씬 힘들어진다. 또한 이러한 전류를 확실히 조절하는 원리가 없기 때문에 확률적인 방법을 통해 측정하게 된다.

이를 위해서 전자가 특정 온도에서 v_th의 속도로만 움직인다 가정하고 이 중 수평 방향인 v_thx만 고려하고자 한다. 그리고 공핍 영역이 굉장히 작다고 가정하여 이를 무시한다. 이는 곧 반도체의 중립 영역과 금속이 곧바로 연결된다는 것을 뜻한다. Ec_M 이상에 존재하는 전자들은 어느 방향으로든 자유롭게 움직일 수 있다. 금속 영역 중 접합면 근처에서 Ec_M 이상에 존재하는 전자는 절반은 반도체 방향으로 나머지 절반은 구 반대 방향으로 움직인다고 가정한다. 이러한 전자의 전체 수를 n_M로 정의하고 금속에서 반도체 방향으로 발생하는 전류를 I_M이라고 정의한다. 이 값은 -q*A*(0.5*n_M)*v_thx와 같다. A느 쇼트키 다이오드의 면적이다. 그리고 이 값이 음수인 이유는 반도체 내에서 전자의 이동 방향과 반대이기 때문이다.
이와 비슷하게 반도체 영역에서는 Ec_M 이상에 존재하는 전자의 수를 n_S로 정의하며 똑같이 절반씩 각 방향으로 이동한다고 가정한다. 그리고 이러한 캐리어에 의해 금속에서 반도체로 흐르는 전류를 I_S로 정의, q*A*(0.5*n_S)*v_thx와 같다.

최종적으로 쇼트키 접합에 전체 전류는 I_MS = I_M + I_S = q*0.5*A*v_thx*(n_S – n_M)이다. 따라서 n_M,과 n_S가 유도된다면 쇼트키 접합에 흐르는 전류를 계산할 수 있다. 열 평형 상태에서 시스템을 통틀어 흐르는 전류가 0이기 때문에 'n_S0 = n_M0' 임을 알 수 있으며 '0'이 이를 의미한다. n_S0는 다시금 페르미 디락 분포, 볼프만 분포를 통해 N_C*e(-q*phi_B/kT)로 계산하며 n_M0는 동일한 값을 가진다.
5) 쇼트키 다이오드의 전류-전압 특성

역방향전압 -Va가 금속에 인가된 경우 금속의 페르미 레벨이 증가한다. 하지만 n_M, 열평형상태에서 n_M0는 전압에 의해 장벽의 높이가 달라지지 않기 때문에 똑같이 유지된다. 반도체 영역에서 n_S는 Ec_M이 페르미 레벨로부터 멀어지기 때문에 감소한다.

이를 통해 n_S의 공식에서 n_S가 n_S0보다 작기 때문에 Va가 음수라는 것을 알 수 있다. n_S와 n_M을 I_MS에 대입한다면 흐르는 전류는 q*0.5*A*v_thx*n_S0*[e(q*Va/kT) - 1)]가 된다. 이 중 bias에 영향을 받지 않는 항들을 따로 묶는다면 우리는 PN 접합 공식과 유사한 식을 얻게 된다. 유일한 차이는 i_0가 도핑이 아닌 쇼트키 장벽의 높이에 영향을 받는다. 역방향전압이 증가되는 경우 쇼트키 장벽이 항복 영역에 진입하게 된다. 쇼트키 장벽이 PN 접합의 공핍 영역에 반만 존재하기 때문에 전자들이 더욱 쉽게 밴드갭을 뚫고 지나간다. 따라서 PN 접합보다 일반적으로 항복 전압이 낮고 제너 항복이 더욱 많이 발생한다.

순방향 전압에서도 역방향과 비슷하게 분석할 수 있다. +Va가 금속에 인가된 경우 내부 전위가 낮아지지만 쇼트키 장벽은 영향을 받지 않는다. 그리고 n_S는 n_S0와 같다. 반도체 영역에서는 Ec_M이 페르미 레벨에 가까워진다. 그리고 새로운 캐리어 농도가 n_S = n_S0*e(q*Va/ kT)로 표현되며 흐르는 전류는 I_MS = q*0.5*A*v_thx*n_S0*[e(q*Va/kT)-1]이다. 역방향 전압과 똑같은 원리이다. 그리고 쇼트키 다이오드의 특징이 PN 접합의 특징과 i_0의 표현 외에 다른 부분에서 굉장히 유사하다는 것을 알 수 있다.
6)쇼트키와 PN 접합의 차이
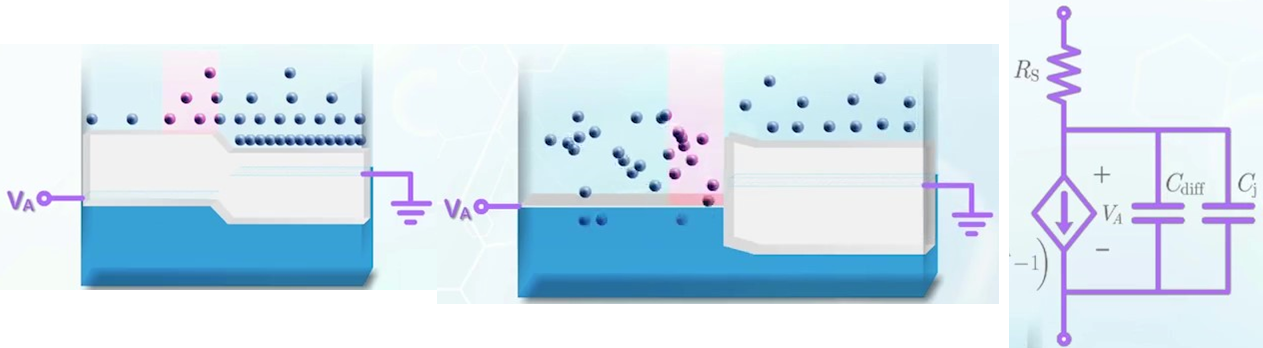
비록 쇼트키 다이오드의 전압 특성이 PN 접합 다이오드와 비슷하지만 그 성능에 있어서는 확연한 차이가 있다. PN 접합에서는 turn-on & off를 위해선 중립 영역의 캐리어 농도가 증가되거나 감소되어야 한다. 이는 확산 커패시턴스 Cdiff에 의해 표현된다. 금속-반도체 접합(쇼트키 접합)에서는 반도체에서 금속 영역으로 전자의 이동이 전자에 흡수되고 캐리어의 저장이 필요하지 않다. 그 결과 Cdiff가 제거되고 굉장히 빠른 turn – on & off가 유도된다. 또한 금속은 어떤 수의 전자를 전부 흡수할 수 있기 때문에 쇼트키 다이오드에 어떠한 high-level injection이 관찰되지 않는다.
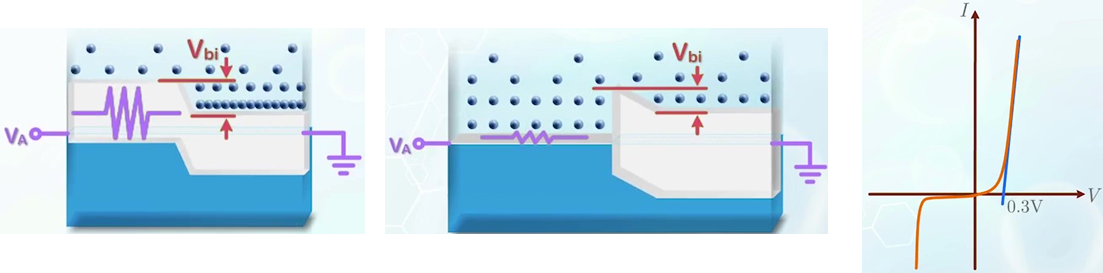
그리고 일반적으로 금속의 저항이 더욱 낮기 때문에 터미널 재료로써 많이 활용된다. 반면에 쇼트키 다이오드의 내부 전위는 일반적으로 PN 접합 다이오드보다 낮다. 구체적인 수치로 실리콘 쇼트키 다이오드의 일반적인 turn-on 전압은 0.3V로 PN 접합의 0.7V보다 크다. 게다가 쇼트키 다이오드는 굉장히 빠른 회로에 적합하다. 그리고 turn-on 전압이 낮을 필요가 있는 회로에서 당연하게도 활용된다. 그 예로 BJT의 클램핑 다이오드가 있다. 이는 다음 BJT 파트에서 더욱 집중적으로 다룰 예정이다. (참고 링크 : https://blog.daum.net/trts1004/12109260) 하지만, 낮은 항복 전압 때문에 높은 전압을 막는 정류기 회로에는 적합하지 않다.
7) 옴 접합

만약 금속이 반도체와 함께 오직 쇼트키 접합만 만들 수 있는 경우, 우리는 몇몇 소자를 활용하는데 문제가 발생한다. 그 이유는 오직 금속을 통해 한 방향으로만 전류가 흐르기 때문이다. 이에 옴 접합을 활용하여 두 방향 모두 전류를 흐르게 한다.

쇼트키 접합의 특징은 다음과 같다. 이를 양쪽 방향으로 흐르게 하기 위해선 역방향 전류가 증가해야 한다. 이는 인가된 전압이 인가되지 않은 상황과 대칭을 이룸으로써 얻을 수 있고 이는 두 가지 방법으로 얻을 수 있다. 첫번째 접근 방법은 n형 반도체 전도대의 가장자리 혹은 p형 반도체 가전자대의 가장자리와 페르미 레벨이 굉장히 비슷한 금속 재료를 사용하는 것이다. 이러한 접합 형태를 선형 접합(linear contact)이라고도 부른다. 이는 전자가 장벽을 통해 자유롭게 움직일 수 있게 해주며 역방향 전압을 증가시켜 준다. 하지만 이러한 방법은 제한이 있다. 그래서 n 혹은 p 중 한 방향에서만 금속을 활용하는 방법을 사용한다. 이러한 방법이 가능한 이유는 전도대에서는 작은 장벽을 이루지만 가전자대에서는 큰 장벽을 형성하기 때문이다. 따라서 n, p 둘 다 금속을 사용하는 경우 양방향으로 전류가 흐를 수 없게 된다.

옴 접합을 형성하기 위한 또 다른 방법은 항복 전압을 굉장히 작은 값으로 낮추는 것이다. 이는 반도체에 고농도로 도핑을 함으로써 얻을 수 있으며 이로 인해 공핍 영역이 굉장히 얇아진다. 이와 동시에 금속의 페르미 레벨은 n형 일 경우 가전자대, p형일 경우 전도대의 가장자리에 가까워 진다. 이는 큰 내부 전위를 유발하고 n형 반도체의 전도대 하단부가 금속의 페르미 레벨에 굉장히 가까워지게 된다. 작은 전압이 시스템에 인가되는 경우, 금속의 전자는 공핍 영역을 쉽게 통과하여 이동하고 반도체의 전도대로 진입한다. 이러한 빠른 항복이 옴 접합을 형성할 수 있게 해준다. 하지만 이는 선형 접합보다 선형성이 떨어진다.

선형과 터널링 접합을 동시에 형성하기 위해서, n,p 형 반도체 동시에 single metal이 사용된다. 예를 들어, 일 함수가 반도체의 가전자대 가장자리에 근접한 금속을 사용함으로써 p 형 반도체에서 선형 옴 접합을 형상한다. 그리고 n형 반도체에 고농도 도핑을 활용함으로써, 터널링 접합을 형성한다. 금속과 반도체 사이에서 옴 접합을 확실히 하기 위해서, 금속과 접합된 반도체 영역이 일반적으로 터널링을 위해 고농도 도핑되며 선형 접합의 저항성을 줄인다. 그 예시가 위와 같다.

이전 까지 배웠던 PN 접합의 에너지 밴드는 사실 아주 정확하지는 않다. 반도체 양쪽 끝단의 열평형상태의 금속-반도체 접합에 대한 내용을 포함하여 에너지 밴드를 다시 그려야 하기 때문이다. 금속과 반도체는 반도체 양 끝단에서 서로 다른 접합을 형성할 것이다. 그리고 내부 전위는 밴드 갭이 휘어짐에 따라 균형을 맞추게 되고 이로 인해서 내부 전위는 측정할 수 없게 된다.