척척학사의 공부노트입니다!
틀린 부분이 굉장히 많을 수 있으며
오류의 정정 및 조언을 해주신다면 정말 감사하겠습니다!
지난 포스트에 이어지는 내용입니다.
[Semiconductor Devices] Physical Bipolar Junction Transistor structures, switching characteristics and model (1)
척척학사의 공부노트입니다! 틀린 부분이 굉장히 많을 수 있으며 오류의 정정 및 조언을 해주신다면 정말 감사하겠습니다! 마지막 7주차 내용 정리 및 번역입니다. 1. Physical structure and switching 1)
nagadi.tistory.com
2. Bipolar Junction Transistor models
1) The Ebers-Moll model

많은 엔지니어는 BJT의 작동 원리보다 제품의 디자인을 위한 특성만 궁금하다. 모델은 이러한 목적 때문에 필요하다. 많은 모델이 가능하지만, 이러한 모델 전부가 경험적인 결과를 정확하게 복사하고자 한다. 때때로, 기본 원리를 이해하도록 제공하는 것이 어려운 경우가 있다. 이러한 대화를 위한 목적으로 BJT의 거동을 설명하기 위해 제일 간단한 Ebers-Moll 모델을 활용해보자.
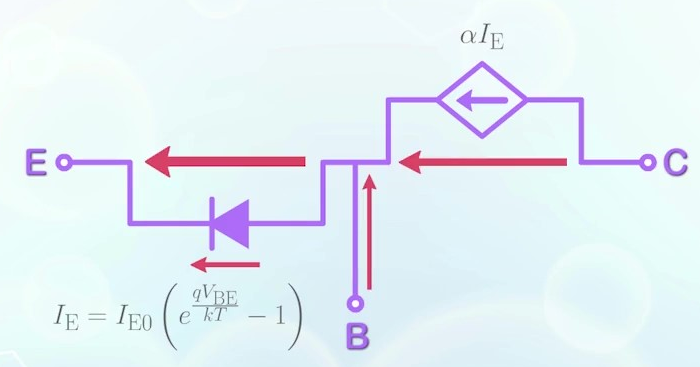
BJT의 작동은 기본적으로 베이스-이미터 사이의 PN 접합이 기반이 된다. 따라서 이 모델에서는 베이스-이미터 터미널에 다이오드를 둔다. 이미터 전류는 다이오드 공식을 통해 알 수 있는 전류와 같다. 이미터 전류의 비율은 알파에 의해 결정되는데 이 값이 콜렉터의 전류가 되고 이는 콜렉터에서 입력 전류에 의해 통제되는 전류 소스로 표현된다. 이 값은 alpha * 이미터 전류이다. 이미터와 콜렉터 전류의 차는 베이스 전류가 된다.

이 모델은 정상 상태의 forward active 모드에서 소자가 어떻게 작동하는지를 설명한다. Reverse active 모드에서 트랜지스터의 작동은 베이스-콜렉터 접합, 또 다른 PN 접합에 의해 동작한다. 앞선 경우과 같이 콜렉터의 전류가 전류 공식을 통해 표현되며 이미터의 전류가 또 다른 전류 소스가 된다. 하지만 forward acitve의 alpha와는 비례항이 다르다. 이를 구분하기 위해 forward active 모드이 alpha를 alpha_F, reverse active 모드의 alpha를 alpha_R로 정의하자.

Forward active 모드에서 베이스-콜렉터 다이오드는 역방향 상태이며 개방회로라고 볼 수 있다. 그렇기에 reverse active 모드와 관련된 요소들은 모두 제거할 수 있다. 비슷하게 reverse active 모드에서 베이스-이미터 다이오드와 관련된 전류 소스를 무시할 수 있다. Cut-off 모드에서 모든 다이오드는 개방회로로 고려되어 어떤 터미널에도 전류가 흐르지 않는다. Saturation 모드에서는 두 다이오드가 베이스로 전류를 흘려보내고 net current는 주입되는 두 전류의 상대적인 크기에 의해 결정된다.

따라서 BJT의 모든 모드를 이 모델을 통해 예측할 수 있다. 하지만 전압의 조절을 통핸 전류 소스의 기능만 표현한다는 사실을 기억해야한다. 동적 거동을 나타내기 위해선 이전에 배웠던 다이오드의 전체 모델을 포함해야 한다. BJT의 서로 다른 터미널에 흐르는 전류가 서로 다르기 때문에, 각 저항들도 상응하는 터미널에 맞게 따로 표현되어야 한다. 하지만 이는 각 다이오드의 동작이 독립되어 있다 가정했기 때문에 굉장히 간략화 한 상황이다. 더욱 디테일한 모델은 더 접합의 영향까지 표현한다. 하지만 기본적인 BJT 동작 이해는 이정도로 충분하다.
2) The small signal model

디지털적인 스위칭 외에도 BJT는 신호 처리 회로에서 일반적으로 쓰이는 증폭기로 활용될 수 있다. 위 이미지와 같은 회로에서, 굉장히 작은 전압 진폭을 가진 전압이 입력된다. 베이스 전압에 따른 콜렉터 전류 변화의 관계를 기반으로 작은 베이스 전압의 변화는 콜렉터 전류의 큰 변화를 유도한다. 콜렉터 전류는 출력 전압으로 전환 될 것이며 이는 Ic * R_L로 표현된다.

이 과정에서 작은 입력 전압의 변화가 반전된 큰 출력 전압 변화를 유도한다. 입력 신호는 일반적으로 작다고 가정한다. 굉장히 작은 입력 신호로 작동 된다면, 회로는 선형 함수와 같은 개형을 보이며 일정 편향된 지점만 고려한 모델만 고려하며 되며 이는 일반적으로 forward active 모드이다. 이러한 모델은 작은 입력신호이지만 넓은 범위의 주파수 대역을 가지는 트랜지스터의 반응성의 학습을 위해 아날로그 회로 설계자에게 굉장히 중요하다.

작은 신호 모델을 구현하기 위해서 베이스-이미터 터미널의 PN 접합을 다시 고려해보자. 큰 신호 모델과 비슷하게 베이스와 이미터 각각에 저항이 분리되어 존재한다. 이미터가 접지되어 있다고 가정하고 r_pi는 위 식과 같이 표현된다. 각 항은 베이스 전류와 베이스 전압의 변화이며 다음과 같은 과정으로 정리할 수 있다. Cje는 베이스-이미터 접합의 커패시터로 그 값을 표현할 수 계산할 수 있다. C_pi는 베이스 전하의 변화로 인한 확산 커패시터로 이도 위와같이 계산할 수 있다. 그리고 이는 dQ_B / dV_BE로 표현된다. 이는 PN 접합에서 Q_B / V_th와 같은 값이지만 BJT 에서는 I_C보다 Q_B라는 표현을 활용하는 것을 선호한다.

베이스에 저장된 전하량은 위 그래프의 색칠된 면적의 전하의 수에 q를 곱한 값과 같으며, forward active 모드에서 Q_B를 식으로 표현할 수 있다. 콜렉터 전류는 베이스에 축적된 전하의 기울기로 표현할 수 있고 이 또한 식으로 표현 가능하다.

n_BE를 제거함으로써 위 식과 같이 정리할 수 있다. 전하와 전류의 관계에 의해서 이는 시간의 단위를 가지게 된다. 이를 베이스 통과 시간(transit time)으로 볼 수 있으며 tau_B로 표현한다. 물리적으로 tau_B는 베이스에서 캐리어가 얼마나 오래 존재하는가를 의미한다. 혹은 이미터에서 콜랙터로 이동하는데 얼만큼 시간이 걸리는 가를 의미한다. 이 값은 일반적으로 10 ps(피코) 정도의 값이 유도된다.

Q_B의 유도를 통해 C_pi를 다음과 같이 정리할 수 있다. dI_C / dV_BE는 베이스-이미터 전압의 변화에 따른 콜렉터 전류의 변화로 측정할 수 있다. 이를 트랜스컨덕턱스(transconductance)라고 칭하는데 그 이유는 컨덕턴스의 단위를 가지고 있기 때문이다. 하지만 이 값은 연결되지 않은 다른 전압에 의해 결정된다. BJT의 선형 동작 기울기를 표현하는 가장 중요한 파라미터로 g_m이라 표현한다. 이어 C_pi는 g_m * tau_B로 표현된다.

콜랙터와 이미터 사이에서 전류는 베이스-이미터 접합의 신호를 통해 조절된다. 이를 전류에 의해 조절되는 전류 소스로 표현할 수 있으며 이러한 경우에 I_C = beta * I_B이다. 혹은 전압에 의해 조절되는 전류 소스를 이용하기도 하는데 이 경우에는 I_C = g_m * v_BE이다. 회로 규칙에 의해 소문자 “v”는 작은 전압의 변화를 나타낸다. 그리고 베타는 다음과 같이 표현할 수 있다. 또한 또 다른 전류 소스로서 Early effect를 유발하는 저항 r_O가 평행하게 연결되며 콜랙터와 이미터를 연결한다.

베이스와 콜렉터 사이에는 역방향 접합의 커패시터 C_mu가 존재하며 접합의 공핍 커패시터를 의미한고 다음과 같이 표현한다. 가끔 C_mu는 전하 Q_B를 V_C에 관한 함수로 포함하는데 그 이유는 베이스의 중립 영역 두께가 감소하기 때문이다. 하지만 그 값이 굉장히 작아 일반적으로 무시된다.

콜랙터와 금속 접합 사이에서도 콜렉터에 저항이 존재하며 이에 r_C가 모델에 추가된다. 마지막으로 콜렉터는 P 기판에 isolation을 위해 둘러 쌓여있고 이는 역방향 바이어스의 공핍 커패시터를 유발한다. 이를 Cd_SC라고 표현한다.
3) Frequency response

트랜지스터가 증폭기로 활용될 때 입력 주파수가 낮을 때 출력이 이를 따라간다. 이 경우에 커패시터는 개방 회로로 고려할 수 있으며 모델에서 전부 제거된다. 트랜지스터 회로의 게인은 상수가 되고 이를 구하기 위해 간략화된 모델을 사용한다.

주파수가 증가하면, 캐리어가 이미터에서 콜렉터로 도달하기전 신호가 반대로 흐를 수 있게 된다. 이는 콜렉터 전류가 입력 신호의 변화에 반응하지 못하는 결과를 유발한다. 따라서 특정 값 이상으로 입력 주파수가 커진다면, 증폭기의 게인은 커페시턴스에 의해 감소하게 된다. 이는 BJT가 정상적으로 작동하는 주파수 범위에 제한을 둔다.

BJT의 속도는 수용가능한 최대 주파수에서 전송 주파수 f_T로 설명된다. 이는 트랜지스터의 주파수가 서로 같아지는 전류 게인, 베타로 정의된다. 만약 베타가 주파수에 대한 로그 스케일로 표현된다면 위와 같은 그래프를 보인다. 낮은 주파수 영역에서 평평하고 고주파 영역으로 들어가면서 값이 떨어진다. 이를 코너 주파수(corner frequency)라고 부른다. 여러 회로 수업에서 베타의 강하는 주파수의 로그 값에 선형이라고 배우며 이 직선을 베타가 일정해지는 지점(1이 되는 지점)까지 연장할 수 있다. 이 주파수를 전달 주파수(transit frequency) f_T라고 부른다. f_T에서 콜렉터의 전류는 베이스 전류와 같아지며 증폭기는 더 이상 입력 신호를 증폭하지 않는다.
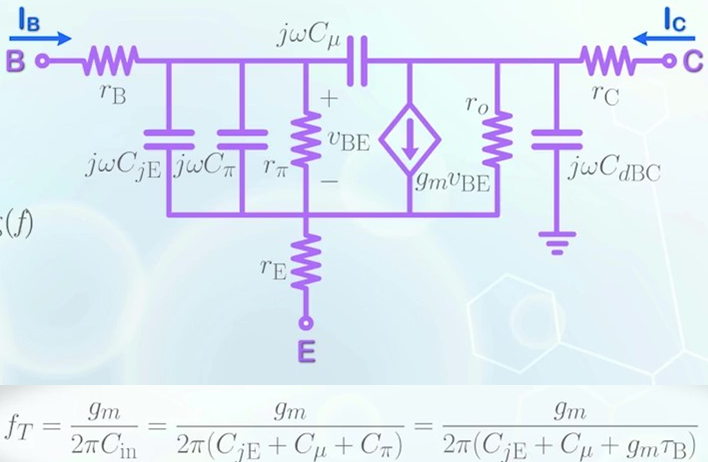
f_T는 작은 신호 모델을 푸리에 변환을 통해 구할 수 있으며 이는 모든 커패시터에 j * w를 곱함으로써 계산한다. 베이스 전류 I_B를 독립 변수로써 주입하고 결과 I_C를 계산함으로써 베타를 I_C / I_B를 통해 w에 대한 함수로 구할 수 있다. 중간 과정을 생략하고 결과만 보자면, C_in은 입력의 커패시터로 f_T의 식을 구할 수 있고 모델을 기반으로 다음과 같은 과정을 통해 식을 유도할 수 있다. 이 중 C_je와 C_u는 큰 변화가 없기에 그대로 둔다.

이 중 가장 중점을 두어야할 부분은 ‘어떻게 f_T가 바이어스 전류로 I_C에 영향을 받느가’이다. 이는 트랜지스터가 빠른 속도를 가지기 위해 어떻게 바이어스를 주어야 하는지 해답을 줄 것이다. I_C가 굉장히 작을 때 g_m 또한 굉장히 작다. 따라서 f_T는 g_m 혹은 I_C에 덜 의존적이다. 그 이유는 분모가 C_je와 C_u에 더 영향을 받기 때문이다. 이후 g_m * tau_B가 접합 커패시터보다 충분히 커졌을 경우, C_je와 C_u는 무시되어 g_m을 소거한 뒤 1/2*pi*tau_B가 된다. 이는 BJT의 최대 작동 주파수가 캐리어가 이미터에서 콜렉터로 이동하기 위한 시간에 의해 제한된다는 것을 알 수 있다. 그 이유는 만약 콜렉터가 신호의 방향이 바뀌기 전에 콜렉터에 도달하지 못한다면, 베이스-이미터 접합 사이를 전자가 양방향으로 이동하더라도 콜렉터의 전류에는 아무런 변화가 생기지 않기 때문이다.

tau_B가 10 ps 범위를 보일 때, f_T는 일반적으로 50~100 GHz의 범위를 보인다. 그리고 I_C가 증가함에 따라 f_T는 감소한다. 그 이유는 f_T는 베타가 일정해지는 경우의 주파수를 측정하며, 이에 high-level injection 영역에 BJT가 진입하면 베타는 감소하기 때문이다.
4) Structural optimization

이후에 배울 MOSFET과 비교해 보았을 때, BJT는 통합된 회로가 아닌 분리된 회로에서 일반적으로 많이 사용된다. BJT의 최대 장점은 높은 전류를 유도할 수 있고 높은 전압을 유지한다는 장점이 있다. 하지만 일반적으로 한 웨이퍼 상에 NPN과 PNP가 동시에 들어갈 수 없으며 이는 상호보완적 구조인 MOSFET과 비교가 된다.

예를 들어 1)일반적인 TTL NOR gate의 schematic을 참고해본다면 오직 NPN 형의 BJT만 활용한다. 2)상호보완적인 BJT 구조도 위 그림처럼 가능하지만 훨씬 복잡하고 선호되지 않는다. BJT 회로의 성능을 향상시키기 위해선 기생 요소를 제거하는 것이 매우 중요하다. 이에 3)좋은 퍼포먼스를 보이는 BJT의 schematic은 다음과 같다. 이 구조에서는 이미터에 N+ polysilicon layer가 추가됨으로써 연장되었고 이는 베이스에서 이미터로 흐르는 확산 정공 전류 줄인다. 베이스에는 P+ 영역이 트랜지스터 외부 영역에 추가되어 베이스 저항을 줄여주었다. 게다가 P+ polysilicon layer가 트랜지스터 구조에서 많은 영역을 소비하는 contact의 포함을 피하기 위해 P+ 베이스와 contact에 활용되었다. 역방향 접합으로 인해 기생 접합 커패시터가 발생하는 대신, 절연체로 구성된 Trench isolation가 구역을 나누는데 활용되었다.
지금까지 Part1에 대한 강의 리뷰를 끝냈다. 기본 물질, PN 접합, BJT에 대한 내용을 다뤘으며 Part2에서는 Field effect transistor와 MOSFET에 대한 내용이 이어진다.
