
Convolutional Neural Networks (CNNs / ConvNets)
CNN은 이전에 다룬 FC와 마친가지로 가중치(weight)와 편향(bias)로 이루어진다. 입력에 대한 스칼라 곱(dot product)와 편한 뒤, 비선형을 취한다.(activation)score 함수는 input 부터 ouput까지 미분 가능한 함수이며. 가장 마지막에선 loss function 이 계산된다. 이전과 차이점은 입력이 이미지이며, 이미지의 특징을 모델이 효율적이고 적은 파라미터로 가볍게 이해할 수 있게한다.
Overview (개요)
FC 에서는 입력을 여러개의 hidden layer를 통해 변형시키며, layer들은 여러개의 뉴런으로 구성된다. layer간의 연결은 각 layer의 모든 뉴런들이 fully-connected되어 동작하며, 동일 layer의 뉴런은 절대 연결되지 않는다. 하지만 이런 FC구조는 일반적으로 이미지 데이터에서 활용되지 않는다.왜냐하면 처리해야할 차원이 너무 크기 때문이다. CIFAR-10 만 해도 32*32*3으로 3072개의 input으로 이루어진다. 이러한 입력을 기반으로 FC가 구성되면 파라미터는 과도해질것이며 굉장히 빨리 과적합 될 것이다.
CNN은 입력이 "너비, 높이, 깊이"의 3차원 input이라는 점을 고려하여 설계된 방법이다.입력과 마찬가지로 뉴런도 똑같이 3차원으로 배열되었다. 또한 이전 레이어의 일부만 활용하며 FC와 같이 이전 모든 뉴런에 연결되지 않는다. 다만 최종 output은 클래스 점수의 단일 벡터로 동일한 형태가 된다. ConvNet에서 각 레이어는 3D input을 미분 가능한 함수를 통해 3D output으로 출력한다.

Layer (레이어)
ConvNet은 레이어의 연속이며, Convolutional, Pooling, Fully-Connected layer을 주로 사용한다. 이러한 레이어가 쌓이며 ConvNet 아키텍처를 형성한다.CIFAR-10을 예시로 Input [32x32x3] - Conv [32x32x12] - ReLU [32x32x12] - Pool [16x16x12] - FC[1x1x10] 처럼 CNN 아키텍처를 구현할 수 있다. 이렇게 하면 ConvNet은 이미지의 픽셀 값부터 최종 클래스 점수까지 레이어 별로 이미지를 변환한다. 여기서 일부 레이어(Conv,FC)는 파라미터가 있고, 일부 레이어(ReLU, Pool)는 파라미터가 없는 경우도 있다. 파라미터들은 정답 레이블을 잘 맞추기 위해 경사하강법을 통해 학습이 수행된다.

Convolutional Layer
Conv layer는 합성곱 네트워크의 핵심이다. Conv layer는 학습이 가능한 필터 세트로 구성된다. 필터의 크기(w * h)는 보통 작으며, input의 모든 depth 를 계산한다.예시로 5x5x3(여기서 3은 입력이 이미지가 보통 RGB 3 채널을 가지기 때문)의 ConvNet의 첫 layer의 filter로 가정하자.
Forwasd pass동안, 필터는 input의 width, height 방향으로 slide하며 스칼라 곱(dot product)를 수행한다. 이렇게 각 위치에서 수행된 스칼라 곱으로 2d의 활성화 맵을 구할 수 있다. Conv layer는 또한 필터 세트이기 때문에 만약 12개의 필터로 이루어지면 12장의 2d 활성화 맵을 얻다. 여러 filter들은 (특별한 패턴이나, 색상, 경계 등 개별로 이미지의 특징을 학습하게되며 전체 12장의 2d 활성화 map을 stack하여 ouput으로 출력한다.
Local connectivity
이미지와 같은 고차원 input을 처리할 때 이전 layer의 모든 뉴런과 뉴런을 연결하는 것은 현실적이지 않다. 대신, 각 뉴런을 input의 지역적인(local) 영역에만 연결한다.뉴런의 이러한 연결은 receptive field라는 하이퍼파리미터이며 그 크기는 filter의 크기 (width, height) 와 동일함. 그리고 Depth 방향으론 input의 depth과 항상 동일하다. 이는 공간의 차원 (w*h)과 깊이의 차원(d)가 비대칭함을 의미한다. (2D 공간은 local, 깊이 공간은 fully)
CIFAR-10에서 [32x32x3] 이미지에 대해, receptive field는 [5x5x3] 이 된다. (5x5는 3x3, 7x7 등이 될 수도 있음) 여기에 bias 1개를 고려하여 receptive field의 파라미터는 5*5*3 + 1 = 76개가 된다.

위 이미지에서 input이 빨간색이고, 첫번째 Conv layer가 파란색으로 시각화되어 있다. input에서 2D 공간으론 일부만 바라보지만, Depth 방향으론 전부 다 사용한다. 파란색 영역의 Depth가 5인 것은 파라미터가 다른 5개의 filter로 이루어진 뉴런이라는 의미한다.FC와 뉴런의 연결 방식만 다를 뿐, 오른쪽 도식화와 같이 dot product, bias, activation 은 동일하게 계산됨.
Spatial arrangement (공간 배열)
Conv 레이어에서 각 뉴런과 input간의 연결성을 살펴보자. Convolution을통해 계산하는 output의 크기는 depth, stride, zero-padding에 의해 결정된다.
- 먼저 output 크기 중 depth는 위에서 봤던 filter의 수다. 각 filter는 서로 다른 이미지의 특징을 학습한다.
- 두번째는 filter가 이동하는 간격인 stride다. Stride가 1이면 filter는 한 픽셀식 움직이며, 2인경우 2픽셀씩 움직인다. 즉, stride가 클수록 output의 크기가 작아진다.
- 마지막으로 zero-padding은 가장자리를 0으로 채우는 것이다. 몇 칸을 채울지는 하이퍼파라미터이며 input의 크기와 ouput의 크기를 유지하기 위해 주로 사용된다. 즉 output의 2D 공간의 크기를 제어한다.
Input 의 크기를 W, Filter의 크기 F, Stride를 S,zero-padding의 양을 P로 지정한다.Input에 대한 output의 크기를 (W-F+2P)/S+1 로 계산할 수 있다.

이를 시각화 한 1D 예제다. 가장 오른쪽에 보이는 박스가 Filter라고 가정하면. F=3. Bias는 0으로 가정이다. Input은 아래며, output은 위쪽으로 Input size W=5, Padding P=1 구조다. 이 중 왼쪽은 Stride S=1으로 위 공식을 사용하면 ( 5 - 3 + 2)/1+1 = 5,오른쪽은 Stride S=2로 위 공식을 사용하면, (5 - 3 + 2)/2+1 = 3 의 output 개수를 구할 수 있다.또한 Stride가 3일 경우, Output의 크기가 정확히 나누어 떨어지지 않으므로 사용하지 않는다. 이처럼 spatial arrangement 파라미터는 제약이 존재한다.
추가 예시로, W=10, F=3, P=0 인 경우, S=2 로 설정하면 (W−F+2P)/S+1=(10−3+0)/2+1=4.5로 정수가 아니다. 실제 코드에서 이런 경우는 오류가 발생하거나, 일부를 잘라내거나, Padding을 강제로 추가하는 등의 조치가 더해진다. 모든 차원이 잘 작동되도록 하이퍼파라미터를 설정해야한다.
앞서 언급한 것과 같이, zero-padding은 입출력의 크기를 맞추기 위해 사용한다. 위 시각화 예제에서도 왼쪽의 경우 input이 5, output도 5로 동일하다. 여기서 zero-padding을 사용하지 않은 경우 output은 3이 되었을 것이다. 일반적으로 S=1일때, zero-padding은 P=(F−1)/2로 설정하면, 입출력의 크기가 동일해진다.
Parameter sharing
Convolutional layer는 파라미터 수를 제어하는 데 사용한다. 예시로 12년 ImageNet 챌린지에서 우승한 Krizhevsky et al의 모델에서는 첫 Conv layer가 55*55*96 = 290,400개의 뉴런으로 이루어지고 각각은 11*11*3 = 363개의 가중치와 1개의 bias가 로 구성된다. 이에 최종 파라미터 수는 290,400*364 = 105,705,600 개다.
이를 하나의 가정으로 파라미터 수를 줄일 수 있는데, 특정 (x,y) 위치에서 어떤 특징이 계산된다면 이는 다른 (x2,y2) 위치에서도 유용하게 활용될 것이라는 가정하는 것이다. (2D 공간에서의 가정) 즉, 96개의 filter들은 각각의 고유한 filter를 1개만 가진다는 것으로,모든 2D 공간 (x,y) ~ (x,y) 에서 동일한 filter로 계산한다.
이러한 parameter sharing으로, 96*11*11*3 + 96 = 34,944개로 가중치를 획기적으로 줄일 수 있다.이렇게 파라미터를 공유하기 때문에 "filter" or "kernel" 이라고 불리며, input과 convolve 되기 때문에 convolution이라 명명한다.

다만, 가끔은 parameter sharing이 합리적이지 않을 수 있다. 예시로, 사람의 얼굴과 같이 특정 위치에서만 특정 정보를 얻어야 하는 경우이다. 동일한 구도의 사람 얼굴 이미지에서 각 기관 별로 특징을 추출하는 것이, parameter sharing으로 얼굴 전체를 동일하게 보는 것보다 유효하다. 이런 경우는 단순한 locally-connected layer를 사용하는 것이 일반적이다.
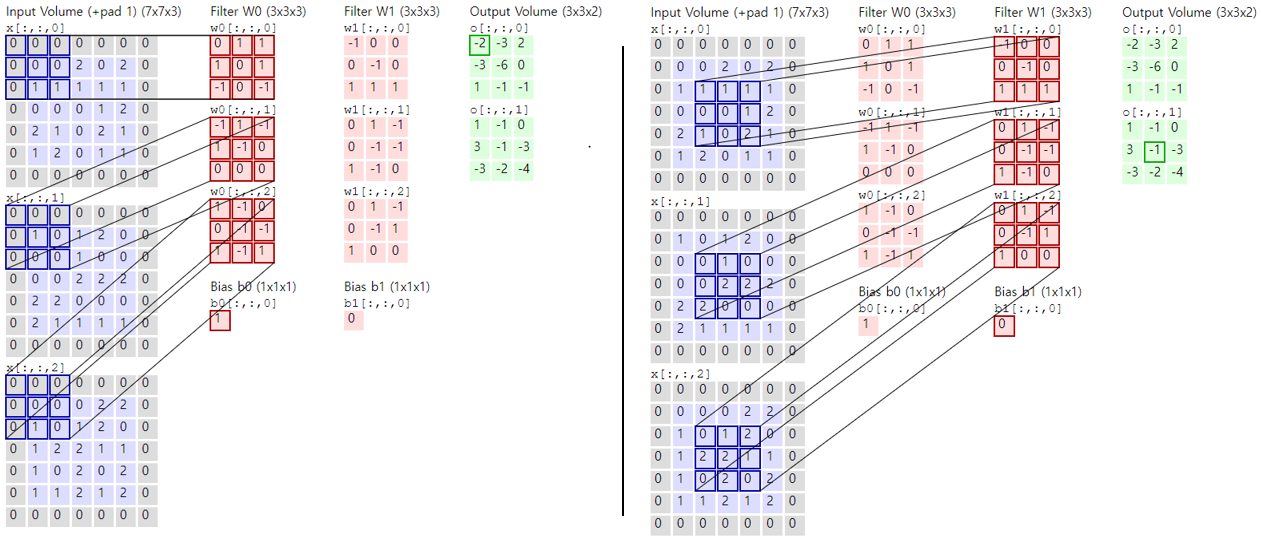
행렬 곱(Matrix Multiplication)으로의 구현
Conv layer는 filter와 input의 local 영역 사이의 내적을 계산한다. 이를 통해 forward pass 는 하나의 큰 행렬 곱으로 구현한다.이를 위해 im2col이라 불리는 작업을 통해 local 영역을 column으로 전환한다.
예시로,[227x227x3] input에 [11x11x3] filter를 stride 4로 사용한다면, (227-11)/4+1 = 55 의 간격을 얻을 수 있다. 이를 토대로 한 filter당 55*55 = 3025번 이미지와 곱해진다. 입력은 filter의 크기인 11*11*3 = 363 만큼 local 별로 추출되어 하나의 열 벡터를 이루면, 최종적으로 [363 X 3025]의 im2col을 얻을 수 있다.
Conv layer도 동일한 방식으로 [96 X 363]의 96개로 이루어진 W_row를 얻는다.(parameter sharing 가정) 이 두 행렬의 곱을 통해 출력은 [96 X 3025]가 되고 이를 다시 [55 X 55 X96] 으로 변환한다. 이는 각각의 local 영역 이미지를 추출하다보니 영역이 중복되어 추출되어 메모리 사용량을 늘린다.허나 행렬 곱이 매우 효율적으로 적용되어 연산 측면에서 유리하다.
Backpropagation (역전파)
Backprop 또한 convolution 연산으로 수행된다. 다만 적용되는 filter는 동일한 filter가 아닌 뒤집힌 filter를 사용한다.
1x1 Conv Layer
몇몇 모델에서는 1x1 컨볼루션을 사용한다. 이는 3차원에서 연산하는 ConvNet 특성상, 1x1의 단순한 filter를 사용해도 input의 depth를 전부 연산하기 때문에 3차원 dot product을 수행한다고 볼 수 있다.
Dliated Convolution
Conv layer에 "dilation"(확장)이라는 하이퍼파라미터를 추가하는 방법이다. 이는 지금까지 배운 "연속되는" Conv filter가 아닌, 각 셀 사이에 "dilation"이라는 간격이 있는 filter를 사용하는 것이다. 예를 들어 filter의 크기가 3 인 경우, w[0]*x[0] + w[1]*x[1] + w[2]*x[2] 가 연속적인 filter 일 때, "Dilation"이 1이면 w[0]*x[0] + w[1]*x[2] + w[2]*x[4]를 계산한다. 이는 공간 정보를 더 집약적으로 사용할 수 있어 일부 상황에서 매우 유용하다.
Pooling Layer
Pooling layer는 일반적으로 Conv layer 사이에 주기적으로 삽입한다. 주 역할은 크기를 점진적으로 줄여 네트워크의 파라미터와 계산량을 줄이고, 이에 따라 과적합을 제어하는 것이다.2D 공간의 크기만 줄이며, Depth를 줄이지는 않는다.
가장 일반적인 형태는 filter의 크기가 2x2이고 stride가 2이며, max 연산을 사용하는 형태. 파라미터는 없다. 이는 width와 height를 1/2로 줄여 75%를 줄여준다. 추가로 일반적으로 zero-padding을 사용하지 않는다.Max 함수로 대부분이 사용되며 거의 2가지 형태를 쓰인다. (F=3, S =2 or F=2, S=2) 이외에도 average pooling이나 L2-norm pooling도 과거엔 사용되었으나 최근엔 사용안되는 추세이다.

Backpropagation 측면에서 pooling layer는 최대값으로 모든 input에 라우팅하면 되기에 매우 간단한 형태다.많은 사람들이 pooling 작업을 싫어하고 없애도 된다고 생각한다.크기를 줄이기 위해 Conv layer에서 큰 stride를 사용하는 것을 제안한다.이는 variational autoencoders (VAEs)나 generative adversarial networks (GANs) 같은 생성형 모델에서 유효하다.
FC -> Conv layer 전환
FC layer와 Conv layer의 유일한 차이점은 Conv layer는 뉴런이 input의 일부 영역에만 연결되어 있고 parameter sharing 가정으로 일부 뉴런들은 파라미터를 공유한다는 것이다. 두 layer는 동일하게 dot product을 사용한다는 점에서 상호 간 변환이 가능하다. 모든 Conv layer는 대부분의 weigth가 0으로 구성되어 있는 FC로 표현할 수 있다.
반대의 경우는, input [7×7×512]에 대해 K = 4096 인 FC layer를 F=7, P=0, S=1, Depth =4096인 Conv layer로 표현한다. 이러한 변환 중 FC -> Conv 는 실제로 유용하다. 224x224x3의 이미지를 7x7x512 로 출력하고, 이후 FC layer를 통해 4096 -> 4096 -> 1000개의 뉴런으로 최종 score 계산를 계산하는 CNN 아키텍처를 가정하자.
여기서 사용된 3개의 FC layer를 Conv layer로 바꿀 수 있다. 첫번째, [7x7x512] 의 input을 filter 크기 F=7을 사용하여 output [1x1x4096]을 생성한다. 두번째, F=1의 filter를 이용 동일한 output [1x1x4096]을 생성한다.마지막도 F=1의 filter이나 다른 depth를 사용 output [1x1x4096]을 생성한다.
이러한 변환은 FC layer의 가중치 W를 Conv layer의 filter로 재구성하는 것이다.또한 Conv layer는 "한번에" 이미지의 여러 위치를 효율적으로 탐색 가능하다. 예시로 [384x384x3]의 input을 동일한 아키텍처에 통과시키면 [6x6x1000]을 얻는다.[384x384x3]를 통한 ConvNet 1번이 [224x224x3]을 추출하여 36번 ConvNet을 수행하는것보다 유리하다. 이는 이미지를 더욱 크게 변환한 후 더 많은 세분화된 공간에서 예측하는 방식이 더 좋은 성능을 보인다.
ConvNet Architectures
Convolutional Networks 일반적으로 conv, pool, fc 그리고 ReLU가 많이 사용된다. 이번엔 이러한 layer 가 어떻게 쌓여 아키텍처를 구성하는지 얘기하고자 한다.
Layer Patterns
이미지가 작은 크기로 줄어들 때까지, Conv-ReLU-Pool을 n번 반복한다.이후 마지막 일부 layer을 FC Layer로 연결하여 최종은 score를 출력한다. (Input -> [[Conv -> ReLU] * n회 -> Pool] * m회 -> [FC -> RELU] * K회 -> FC) 특히, Pool 전에 n 번 Conv를 진행하는 것은 복잡한 연산도 가능하게 하여 더욱 크고 깊은 네트워크를 형성하기 위해 도움이된다.
Conv의 filter는 되도록 작은 것을 선호한다. 예시로 3개의 3x3 Conv-ReLU layer를 사용하는 것과 1개의 7x7 Conv layer를 사용하는과 동일한 효과를 가진다.또한 activation 함수의 개수 차이로 3개의 layer가 더 많은 비선형성을 포함하여 많은 특징을 담을 수 있다. 또한 Depth 가 전부 C라고 가정하면 3x3의 3개 layer는3×(C×(3×3×C))=27C^2,7x7 layer는 C×(7×7×C)=49C^2의 파라미터수를 가지기에, 파라미터 수 관점에서도 유리하다.다만 3개의 3x3 Conv는 backprop 때 더 많은 메모리를 사용한다는 단점이 있다.
다만 이러한 직선적인 구조는 최근에는 사용되지 않는다. 구글의 Inception이나, 마이크로소프트의 ResNet 과 같은 다른 형식의 연결 방식이 선호된다. 사실 현실적으로 이러한 아키텍처를 직접 구현하는 것보단, 잘 구현되어 있는 미리 학습된(pretrained) 네트워크를 다운 받아 데이터에 맞게 fine-tune 하여 사용하는 것이 효율적이다.
Layer Sizing Patterns
아키텍처와 관련된 일반적인 하이퍼파라미터 및 각 기준을 알아보자.
- Input layer의 크기는 2로 많이 나눌 수 있는 것이 좋으며. 32, 64, 96, 224, 384, 512 등이 자주 사용된다.
- Conv layer는 3,5의 작은 filter를 사용하며, stride는 1을 사용. 또한 2D 공간 width, height를 변경 하지 않는 zero padding을 사용함. (F=3 -> P = 1 / F =5 -> P = 2) 7 이상의 큰 filter는 이미지를 입력으로 받는 첫 layet에선 종종 사용되기도 함.
- Pool layer는 2D 공간의 크기를 줄이는데 사용됨. 가장 일반적으론 F=2, S=2 의 Max pooling이 사용됨.이는 전체 크기의 75%를 줄여줌. 가끔 F=3, S=2, P=1의 pooling도 사용하긴 하나, 정보 손실이 심하며 굉장히 공격적인 방법으로 빈도는 거의 드뭄.
위 Guide는 Conv layer가 input의 크기를 유지하면서, Pool layer만 크기를 다운샘플링한다. Stride를 1보다 키우거나, zero-padding을 사용하지 않는 다른 구조는 이미지가 처음부터 끝까지 빠지는 부분 없이 잘 전달되는지 검토해야한다. 예를 들어 Stride가 커서 중간에 생략되거나, zero-padding이 없어 이미지 가장자리가 crop되는지 확인한다. 이러한 관점에서 이미지의 고른 사용을 위해 stride는 1을 권장하며 stride를 늘리기보단 pool layer 추가가 더 좋다.
Zero-padding 또한 입력의 크기를 유지시키는 목적이 있으나, zero-padding 없이 여러 conv layer를 통과하면 이미지 외곽의 정보는 빨리 "사라져" 버리는 부효과도 생긴다. 또한 현실적인 메모리 제약의 측면에서 이미지가 input으로 활용되는 첫 layer는 큰 filter와 큰 stride를 사용하기도 한다. 예시로 ZF Net에선 F=2, S=2의 Conv layer, AlexNet에선 F=11, S=4의 Conv layer를 첫 layer로 활용한다.
Case Study
- LeNet.성공적인 결과를 보인 첫CNN 모델이다.1990년대 Yann LeCun에 의해 개발.우편 번호, 숫자 등을 읽는 데 사용한다.
- AlexNet.CNN을 유명하게 만들어준 모델이다. LeNet과 매우 유사한 아키텍처이나 더 깊고 크고, 여러 Conv Layer가 서로 쌓인것이 특징이다. 이전에는 단일 Conv에 즉시 Pool을 사용하는 것이 일반적이었다.
- ZF Net.Zeiler & Fergus Net의 약자로,하이퍼파라미터를 조정하여 AlexNet을 개선했다.
- GoogLeNet.파라미터 수를 크게 줄이는 Inception 모듈이 사용된 모델이다. (4M, AlexNet은 60M). 또한 이 논문은 FC layer 대신 Average Pooling을 사용하여 중요하지 않아 보이는 많은 파라미터를 제거했다. GoogLeNet에는 최신 버전인 Inception-v4도 있다.
- VGGNet.네트워크의 깊이가 좋은 성능에 대한 중요한 구성 요소임을 보여 준 모델이다. Conv/FC가 16개로 구성된 CNN이 최고의 성능을 보여줌.단점은 파라미터가 너무 많다는 것(140M)이며, 다만 이는 FC layer를 제거함으로써 그 수를 많이 줄이면서 성능 하락은 거의 없이 사용 할 수 있다.
- ResNet. Residual 학습에 이용되는 skip connection이라는 특별한 구조와 batch normalization을 사용한 것이 특징인 아키텍처다. 또한 마지막 FC layer도 사용되지 않음. 현재 Skip connection은 CNN에 기본적으로 사용하는 구조 중 하나다.
자세한 Case Study는 별도의 Category로 추가 연재할 예정.
Reference
CS231n 강의 노트 : https://cs231n.github.io/convolutional-networks/
'딥러닝 > Basic (CS231n)' 카테고리의 다른 글
| [CNN] Transfer Learning, Fine-tuning (0) | 2024.06.29 |
|---|---|
| [CNN] CNN의 시각화 (0) | 2024.06.22 |
| [CNN] Softmax classifer vs Neural Network Case Study (2) | 2024.06.08 |
| [CNN] Optimizer (Momentum, Nesterov, RMSprop, Adam...), Hyperparameter tuning, Evaluation (0) | 2024.06.01 |
| [CNN] Gradient check, 모델 학습 지표 (0) | 2024.05.25 |