
Case study
2차원의 데이터를 기반으로 한 신경망 구현을 예제로 살펴볼 예정이다.신경망 이전에 간단한 선형 분류기를 구현하고 일부 수정하여 2-layer Neural Network로 발전시켜보고자 한다.
Dataset 생성
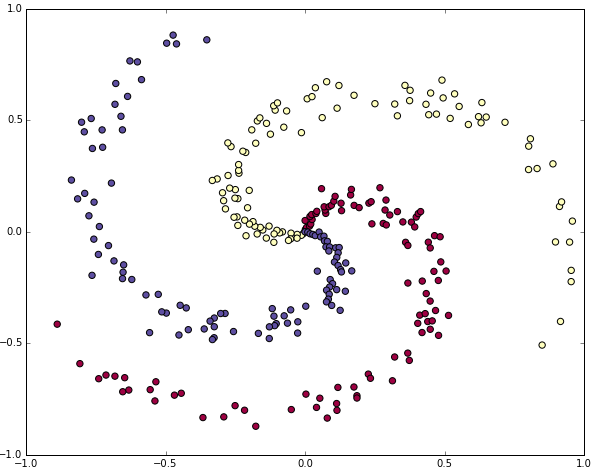
선형적으로 생성하기 어려운 데이터를 생성해보자. 선형적으로 분리되지 않은 파란색, 빨간색, 노란색 3개의 클래스로 구성되어있다. 일반적으로 평균이 0이고 표준 편차가 1인 데이터를 전처리를 하나, 이 데이터의 경우 -1 ~ 1의 적절한 범위에 있으므로 전처리는 건너뛴다.
Softmax linear classifier 학습
Softmax classifer는 linear score function과 cross-entropy loss를 사용한디. 파라미터는 각 클래스에 대한 가중치 행렬 W와 bias 벡터 b가 있다. 초기화는 random number로 수행한다.
클래스 별 score 계산
Linear classifier 특성 상 행렬 곱 scores = np.dot(X, W) + b을 통해 모든 클래스의 점수를 간단하게 한번에 계산 가능하다.예제 데이터가 300개의 점으로 이루어진 데이터셋이므로, scores 행렬은 [300x3] 의 크기를 가진다. 각 행은 3개의 클래스(파란색, 빨간색, 노란색)에 해당하는 클래스 점수를 의미한다.
Loss 계산
Loss는 score의 불일치 정도를 계산하는 미분 가능한 함수다. 올바른 클래스가 다른 클래스보다 더 높은 점수를 가지길 원한다. 이 경우에는 손실이 낮고 그렇지 않으면 손실이 커진다. 이를 quantify(양적화) 하는 방법은 많으나, Softmax classifier에서는 cross-entropy loss를 활용한다.
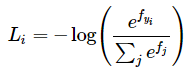
f는 단일 sample에 대한 클래스 별 점수를 담은 배열이다. Softmax classifer는 f의 각 요소를 각 클래스의 unnormalized한 로그 확률로 간주한다. 이에 f에 exp를 취하여 unnormalized한 확률을 구하고 이를 normalize하여 최종 확률을 구한다. 이는 항상 0~1 사이의 값을 가지며, 올바른 클래스의 확률이 0에 가까워 질수록 loss는 무한대에 가깝게 커진다. 반대로 올바른 클래스의 확률이 1에 가까워지면 loss는 0에 수렴하게된다.
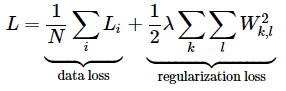
최종적으로 사용할 loss는 batch내 모든 sample의 cross-entropy loss를 평균한 값과 regularization으로 구성된다. 이렇게 계산된 loss를 최소화하면 올바른 클래스에 대한 확률이 높아지게 될 것이다.
Backpropagation을 통한 analytic 기울기 계산
SGD를 통해 Loss를 최소화한다. 파라미터에 대해 무작위로 초기화를 수행하고, Loss에 대한 파라미터의 기울기를 계산한다.이를 활용하여 loss를 줄이는 방향으로 가중치를 변경한다.

p는 클래스 별 확률을 나타내는 벡터이며, Li는 이를 통해 계산한 loss이다. Li를 줄이기 위해 fk 가 어떻게 변경되어야 하는지가 중요하다. 이는 곳 ∂Li/∂fk (Li의 f 에 대한 편미분)을 구해야한다는 것. 이는 Li의 f로 구성된 p에 대한 편미분으로 계산 가능하다.
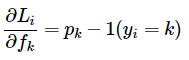
Chain rule을 통해 구한 단순화된 식은 위와 같다. 확률이 p = [0.2, 0.3, 0.5] 라고 가정하고 두번째 0.3이 정답이면, score에 대한 기울기는 df = [0.2, -0.7, 0.5]이다. 즉, 올바른 클래스의 확률이 증가(-0.7 -> 0)하면 loss에는 반대 방향으로 영향을 주어 loss는 감소하게 된다.
파라미터 업데이트 수행
Loss를 줄이기 위해 음의 기울기 방향으로 파라미터 업데이트를 수행한다.
Softmax classifier 전체 코드
# Softmax Classifier 예지
# random number 초기화
W = 0.01 * np.random.randn(D,K) # D:2 (차원), K:3 (클래스 수)
b = np.zeros((1,K))
# 하이퍼파라미터 설정
step_size = 1e-0 # learning rate
reg = 1e-3 # regularization strength
# iteration 설정
num_examples = X.shape[0]
for i in range(200):
# 클래스 별 score 계산, [N x K]
scores = np.dot(X, W) + b
# 클래스 별 확률 계산(probs)
exp_scores = np.exp(scores)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K]
# loss 계산
correct_logprobs = -np.log(probs[range(num_examples),y])
data_loss = np.sum(correct_logprobs)/num_examples # 평균 cross-entropy loss
reg_loss = 0.5*reg*np.sum(W*W) # regularization
loss = data_loss + reg_loss
if i % 10 == 0:
print "iteration %d: loss %f" % (i, loss)
# Loss의 score에 대한 기울기 계산
dscores = probs
dscores[range(num_examples),y] -= 1
dscores /= num_examples
# backprop (역전파)
dW = np.dot(X.T, dscores)
db = np.sum(dscores, axis=0, keepdims=True)
dW += reg*W # regularization
# 파라미터 업데이트
W += -step_size * dW
b += -step_size * db<print>
iteration0:loss1.096956
iteration10:loss0.917265
...
iteration170:loss0.786373
iteration180:loss0.786331
iteration190:loss0.786302
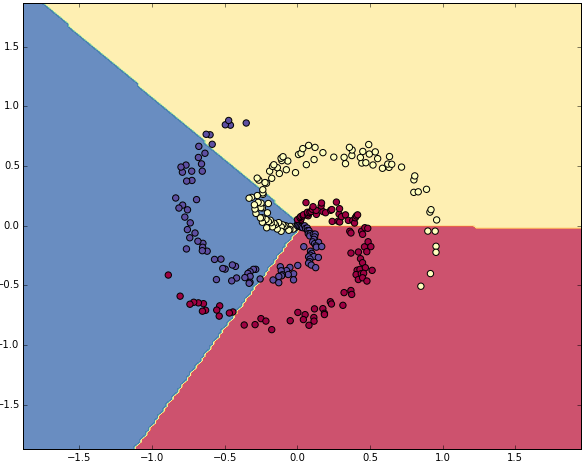
중간이 생략되었으나, 총 iter를 수행한 후 학습은 충분히 수렴하였다. Accuary로 점수를 계산하면 49% 가 나오며, 언뜻 수치는 낮아보이나 선형 dataset이 아님을 감안하면 충분히 좋다.클래스별 결정 경계는 아래와 같다.
Neural Network 학습
예제 데이터는 1개의 hidden layer(Output layer까지2-layer 신경망)로 구분이 가능하다. 각 layer 별 Weights, bias를 미리 추가해 두어야한다. (W,b,W2,b2 변수 추가) score 를 계산하기 위한 forward pass는 hidde_layer + ReLU로 구성된다.
이후 나머지는 softmax classifer와 동일하다. 변경된 가중치의 형태에 따라 역전파 방식만 변경 필요하다. 이 과정에서 ReLU에 대한 기울기도 고려해야 하며, ReLU는 r = max(0, x)이므로 dr/dx = 1 (x > 0)이다. 이에 Chain rule에서 ReLU는 input이 0보다 크면 기울기를 유지, 0보다 작으면 0 으로 지운다. 각 Weights, bias의 기울기 행렬도 최종적으로 추가된다.(dW,db,dW2,db2)
# random number 초기화
h = 100 # hidden layer의 뉴런 수
W = 0.01 * np.random.randn(D,h) # D:차원, h: 뉴런 수
b = np.zeros((1,h))
W2 = 0.01 * np.random.randn(h,K)
b2 = np.zeros((1,K))
# 하이퍼파라미터 설정
step_size = 1e-0 # learning rate
reg = 1e-3 # regularization strength
# iteration 설정
num_examples = X.shape[0]
for i in range(10000):
# 클래스 별 score 계산, [N x K]
hidden_layer = np.maximum(0, np.dot(X, W) + b) # ReLU 추가 (max(0,-))
scores = np.dot(hidden_layer, W2) + b2
# 클래스 별 확률 계산
exp_scores = np.exp(scores)
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K]
# loss 계산
correct_logprobs = -np.log(probs[range(num_examples),y])
data_loss = np.sum(correct_logprobs)/num_examples # average cross-entropy loss
reg_loss = 0.5*reg*np.sum(W*W) + 0.5*reg*np.sum(W2*W2) # regularization
loss = data_loss + reg_loss
if i % 1000 == 0:
print "iteration %d: loss %f" % (i, loss)
# score의 기울기 계산
dscores = probs
dscores[range(num_examples),y] -= 1
dscores /= num_examples
# backprop 진행
# W2, b2에 대한 backprop
dW2 = np.dot(hidden_layer.T, dscores)
db2 = np.sum(dscores, axis=0, keepdims=True)
# hidden layer에 대한 backprop
dhidden = np.dot(dscores, W2.T)
# ReLU 의 기울기 반영
dhidden[hidden_layer <= 0] = 0
# W,b에 대한 backprop
dW = np.dot(X.T, dhidden)
db = np.sum(dhidden, axis=0, keepdims=True)
# regularization 추가
dW2 += reg * W2
dW += reg * W
# 파라미터 업데이트
W += -step_size * dW
b += -step_size * db
W2 += -step_size * dW2
b2 += -step_size * db2iteration0:loss1.098744
iteration1000:loss0.294946
...
iteration7000:loss0.245400
iteration8000:loss0.245335
iteration 9000: loss 0.245292
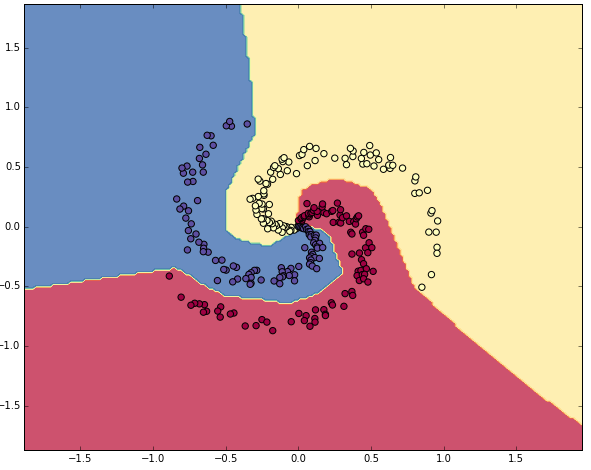
충분히 수렴하였으며, 정확도는 98%로 성능이 매우 뛰어나다. 클래스 별 결정 경계는 아래와 같다.
Reference
CS231n 강의 노트 : https://cs231n.github.io/neural-networks-case-study/
'딥러닝 > Basic (CS231n)' 카테고리의 다른 글
| [CNN] CNN의 시각화 (0) | 2024.06.22 |
|---|---|
| [CNN] Convolutional Neural Networks (CNN) (2) | 2024.06.15 |
| [CNN] Optimizer (Momentum, Nesterov, RMSprop, Adam...), Hyperparameter tuning, Evaluation (0) | 2024.06.01 |
| [CNN] Gradient check, 모델 학습 지표 (0) | 2024.05.25 |
| [CNN] Preprocessing (전처리), Weight init (가중치 초기화), Loss function (손실 함수) (0) | 2024.05.18 |