
Data와 Model 설계하기
뉴런은 비선형성이라는 특징이 있으며 dot product을 수행한다. 신경망은 이러한 뉴런들로 이루어진 여러 layer로 구성된다. 신경망은 새로운 형태의 score function로 정의할 수 있다. 선형과 비선형의 번갈아가며 계산된다.신경망을 학습하는데 data preprocessing, weight initialization, loss function 의 설계를 고민해야한다.
Data preprocessing (데이터 전처리)
데이터 전처리는 크게 3가지로 수행될 수 있다. 행렬 X를 전처리한다고 가정, X의 크기는 [N X D]이며 N은 데이터의 수, D는 데이터의 차원이다.
Zero-centerd (원점 이동)
Zero-centered은 전체 데이터의 각 차원 별 평균을 빼는 것을 의미한다. 이는 데이터의 모든 차원을 원점으로 중심화. X -= np.mean(X, axis=0) 로 구현 가능하다.
Normalization (정규화)
Normalization은데이터의 모든 차원을 동일한 척도로 만드는 것을 의미한다. 크게 두가지 방법으로 수행된다. 하나는 각 차원을 중심화한 후 각 차원을 해당 표준 편차로 나누는 것. X /= np.std(X, axis=0) 로 구현 가능하다. 둘은 데이터의 각 차원이 min -1 max 1이 되도록 하는 것이다.
Normalization은학습을 진행하며 각 차원이 동일한 중요성이 있어야 하는 경우에만 적용하는 것이 합리적이다.모든 차원의 Scale이 동일하다면 필수적으로 수행할 필요는 없다.

PCA and Whitening
# input 행렬 X 의 크기 [N x D]
X -= np.mean(X, axis = 0) # zero-centered
cov = np.dot(X.T, X) / X.shape[0] # 공분산 계산
U,S,V = np.linalg.svd(cov)
Xrot = np.dot(X, U) # 기존 data 투영
# whitening -> eigenvalues로 나눔
Xwhite = Xrot / np.sqrt(S + 1e-5) # 0으로 나뉘는 것을 방지분산이 없는 차원을 버리고 상위 몇 개의 고유 벡터만 사용하는 것을 Principal Compnent Analysis(PCA)라고 한다. raw data X가 원점으로 중심이 이동한 후, covariance matrix (공분산) 을 계산한다.cov(공분산)의 (i, j) 요소는 데이터의 i번째 및 j번째 차원 간의 공분산을 의미한다. cov로 SVD 분해 (특이값 분해)를 수행할 수 있다.


U의 열은 eigenvector(고유 벡터), S는 singular values(특잇값)의 1차원 배열, V의 열은 변환 전 직교 벡터이다. 이후 원 데이터 X를 eigenbasis(고유 기저)로 투영하며 이는 데이터가 고유 벡터가 새로운 축인 데이터로 회전됨을 의미한다. 이 과정을 통해 eigenvalue(고유값)로 정렬되어 차원이 축소된다.
이에 Xrot_reduced = np.dot(X, U[:,:100]) 와 같이 상위 일부 차원만 사용해도 가능하며, 그 이유는 상위 일부에 대부분의 분산이 포함되기 때문이다. 용량과 시간, 연산의 관점에서 아주 좋은 방법이다.
마지막으로 whitening을 수행한다. Eigenbasis로 투영된 data를 차원별 eigenvalue로 나누어 정규화(normalize)하는 방법이다.결과적으로 whitening 까지 수행된 data(raw가 Gaussian 일 때)는 평균이 0, 분산이 공분산인 Gaussian 형태가 된다. 이 변환의 단점은 노이즈를 크게 과장할 수 있다는 점이다. 모든 차원을 동일한 크기로 변환하기 때문이다.이는 0으로 나뉘는 것을 방지하기 위해 더한 1e-5를 좀 더 큰 수로 증가시키는 방법으로 완화 할 순 있다.

CIFAR-10 이미지으로 이러한 변환을 수행한 예시다.Training set은 [50,000 x 3072]의 data이며, 아래는 그 중 49개의 이미지에 대해 시각화하였다.

- original image는 3072차원이며, PCA로 구한 3072개의 eigenvector 중 상위 144개만 선정하였다.
- reduced image는 PCA를 사용하여 차원이 감소된 이미지다. 시각화를 위해선 3072차원으로 다시 원상 복구해야하나, 학습에는 144차원의 data를 활용한다.
- 마지막은 whiten까지 반영된 결과다. 이 역시 PCA 까지 적용된 이미지와 동일하게 시각화를 위해 3072차원으로 복구되고 학습은 144차원 data를 활용한다.
다만, PCA/Whiteing은 CNN에서 자주 사용되지 않는다. Zero-centered와 normalization만 주로 수행된다. 마지막으로, 전처리를 하는 경우 train, val, test 별로 전처리를 하는 것이 아닌, train 에서 계산된 통계량 (mean, std 등)을 다른 val, test에 적용하여 전처리를 해야한다.
Weight initalization (가중치 초기화)
네트워크를 훈련시키기 전에는 파라미터를 초기화해야한다. 이전 등산가 비유법에서 등산가의 초기 위치는 랜덤이라는 점과 의미가 같다.가장 쉬운 실수는 전부 0 혹은 동일한 값으로 초기화 하는 것이다.모든 w가 0이면 모든 뉴런은 동일한 출력을 계산하고, backprop 중 모두 동일한 기울기를 계산하여 w가 동일하게 학습되게 된다. 이는 곳 뉴런간의 차이가 없어지게 된다.
따라서 가중치 w는 0에 가까워야 하지만, 0 혹은 동일한 값이 되어서는 안된다. 모든 뉴런을 다음 layer의 "모든" 뉴런에 연결한 것이 아닌(FC), "일정 수의" 뉴런에 "무작위로" 연결한 경우 가중치 행렬을 모두 0으로 설정 가능하다. 이를 Sparse initialization 라고 한다.
이에 작고 서로 다른 임의의 수로 초기화하는 것이 일반적이다. 모든 뉴런이 무작위하고 고유하다는 것을 반영한다. 이후 학습을 통해 뉴럴들 스스로 전체 네트워크의 다양한 부분으로 통합될 것이다. 다만 작으면 작다고 좋은 것은 아니다. 이는 똑같이 굉장히 작은 기울기를 계산할 것이며, 기울기의 전파를 약화시킨다.
또 다른 방법은 임의로 가중치의 분산을 1/√n로 보정하는 것이다.(n = 해당 뉴런의 입력 수) output의 분포는 input 개수에 따라 증가하며, 뉴런의 출력 분산을 1로 정규화하기 위해 보정을 취하는 것이다. 네트워크의 모든 뉴런이 대략 동일한 출력 분포를 가지게 되며, 수렴 속도가 실험적으로 향상된다. s를 가중치 w와 입력 x사이의 dot product로 고려하며, 이는 곧 activation function 전 cell body에서 수행되는 연산과 같다.
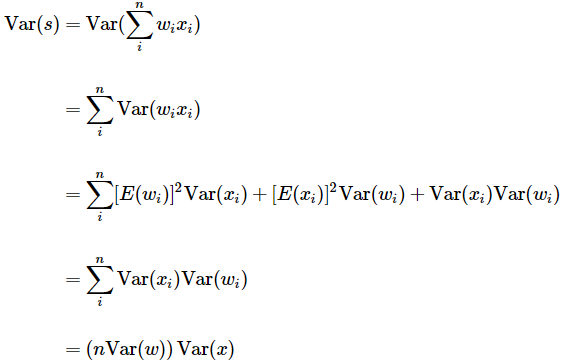
s의 분산은 위와 같다.Var(s) = Var(x) 가 되려면, Var(w)이 1/n 이 되어야 한다는 것을 확인할 수 있다. 이 외에도 Var(w)=2/(nin+nout) (nin : 전 layer의 뉴럴 수. nout : 다음 layer의 뉴럴 수) 초기화 방법, ReLU 뉴럴에 맞춘 w = np.random.randn(n) * sqrt(2.0/n) 를 사용한 초기화 방법 등 다양한 방법론이 존재한다.
Bias는 모두 0으로 초기화하는 것이 가능하고 일반적이다. 왜냐하면 가중치 w가 서로 다르면 b는 서로 다른 방향으로 훈련이 되기 때문이다. ReLU가 사용되는 경우 기울기를 전파하기 위해 0.01 과 같은 작은 양의 상수 값을 사용하기도 한다.
Batch Normalization은 신경망 초기화하며 발생한 문제를 완화시켜준다.이는 학습이 시작될 때부터 네트워크 내 전체 활성화 함수의 input이 Gaussian 분포가 되도록 강제한다.Normalization은 간단한 미분 가능한 연산으로 신경망에 추가가 가능하며 주로 Activation (비선형성) 전에 추가한다.
Regularization
L2 regularization


가중치의 제곱한 크기만큼의 페널티를 부여함으로써 구현할 수 있다. λ는 regularization strength(강도). 1/2를 곱하는 이유는 기울기가 λ * w 로 표현되기 때문이다. L2 regularization는 가중치가 고르게 분산되게 해주는 효과가 있다. 이는 입력의 일부만 사용하기 보단 전부를 골고루 사용할 수 있게 유도한다.
L1 Regularization

가중치의 절대값을 페널티로 부여한 형태다. L1 regularization 는 가장 중요한 몇몇 개의 입력만 사용하고 "잡음"으로 판단되는 입력에는 영향을 받지 않는다. "잡음"에 해당하는 가중치가 거의 0에 가까워지게 된다. L1 + L2 도 가능하며 이를 Elastic net regularization 이라고한다.
Max norm constraint

Max norm constraint는가중치의 크기에 절대 상한을 강제하는 방식이다. 이를 위해 투영된(projected) 경사하강법을 사용한다. 가중치를 업데이트한 후, 가중치 벡터가 c를 넘지 못하도록 클램핑(clamping)하는 것이다. (일반적으로 c는 3 or 4) 이는 learning rate가 큰 경우 가중치가 "폭발"(explode) 해버리는 것을 방지한다.
Dropout (드롭 아웃)
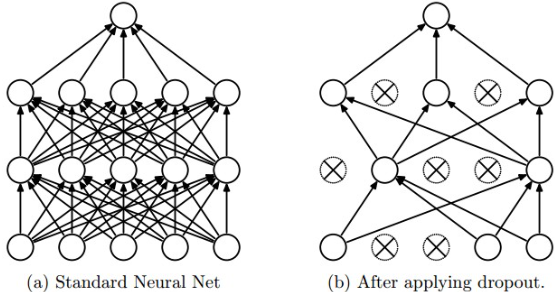
p(하이퍼파라미터)확률로뉴런을활성화시켜,훈련중일부만학습되게하는방법이다.매 훈련마다 각 노드가 확률적으로 학습이 되거나 안되며, 이는 신경망 중 일부 가중치를 샘플링하여 훈련한다고 해석한다.
입력 레이어에서도 드롭아웃 수행 가능하지만 테스트 중에는 드롭아웃이 적용되지 않는다. 다만 hidden layer의 output에 확률 p를 곱해줘야 하는데, 이는 p%의 뉴런만 사용하는 훈련 테스트와 동일한 scale로 맞춰주기 위함이다. 즉, 훈련 시 dropout으로 인한 출력은 p * x + (1 - p) * 0 = p * x 이며, 테스트에서는 dropout이 없다. 이를 동일하게 맞춰주기 위해 일부러 p를 추가로 곱한다. 또한 Dropout은 매번 새로운 뉴런이 제외되기 때문에 서로 다른 모델의 ensemble(앙상블) 예측 처럼 볼 수도 있다.
Inverted dropout은 테스트에서 p를 곱해주는 것을 훈련시에 1/p를 곱해주는 것이며, 테스트 시 속도적인 관점의 성능이 중요하기에 사용한다. Dropconnect은 임의의 가중치 집합이 대신 0으로 설정되는 것으로, CNN에서 stochastic pooling, fractional pooling, data augmentation 등에 사용된다. Bias regularization 는 사실 일반적이지 않은 방법이먀, 데이터와의 곱셈 상호 작용을 통해 상호 작용하지 않기 때문이다. Per-layer regularization 는 층별로 다른 크기로 정규하는 것이며, 이 또한 자주 사용되는 방법은 아니다.
Loss function
Loss function은 (지도 학습 + classification을 가정하여) 예측과 정답 간의 차이를 측정하는 함수다. Loss는 Batch의 각 Sample 별 loss의 평균으로 계산된다. Classification에서 dataset 은 sample의 집합이며, sample 별로 하나의 정답 레이블이 있다고 가정하자.
SVM (hinge loss)
이 가정으로 구할 수 있는 간단한 loss function은 SVM 이 있다. Hinge loss의 제곱이 성능이 더 좋다는 결과도 있다.

Cross-entropy loss

Cross-entropy loss를 이용한 Softmax도 가장 많이 사용되는 loss function 중 하나다. 다만 클래스의 개수가 매우 큰 경우 (ex : 영어 사전의 단어), 단순 Softmax를 사용하는건 과도한 연산량을 요구한다.
Hierarchical Softmax
Softmax의 응용한 버전, 자연어 학습과 같은 경우에 사용된다. 각 레이블(단어)는 tree를 따라 경로가 표시되고 classifier는 각 노드에서 왼쪽 or 오른쪽으로 흐를지 훈련한다.
Attribute classification
단일 레이블이 아닌, 여러 레이블(멀티 레이블)에서 사용된다. 예시로 인스타그램의 사진들은 모든 해시태그 들 중 일부를 포함하고 있다. 이 해시태그를 Attribute (속성) 이라고 가정한다면, 레이블은 사진들의 개별 attribute(해시태그) 별 binary classifier로 표현 할 수 있다.

yij는 예제가 j번째 속성으로 레이블이 지정되었는지에 따라 +1 또는 -1로 계산된다. 스코어 벡터 fj는 클래스가 존재할 때 양수이고 그렇지 않으면 음수이다. 해당되는 속성의 점수가 +1보다 작거나, 해당되지 않는 속성의 점수가 -1보다 큰 경우 손실이 누적된다.
Binary logistic regression classifier
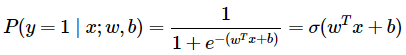
동일하게 여러 레이블의 경우에 활용될 수 있다. 이는 두 가지 클래스(0,1)만 가지고 있으며, 각 레이블 별 classifier가 따로 계산된다. Classifier의 값은 레이블에 해당되는 속성이면 1, 해당되지 않는 속성 0이 된다.위 식은 클래스 1에 대한 확률 계산식. 클래스 1과 0 의 확률의 합은 1이며 각 계산 값은 항상 0이상이다. 이러한 확률 값의 범위를 감안해, 확률에 -log를 취해 사용함으로써 loss function 에 사용된다.
Regression (회귀)

특정 실수 값으로의 예측하는 작업이다.예측과 실제 사이의 loss를 계산한 다음, 그 차이의 L2 squared norm 또는 L1 norm을 계산하는 것이 일반적이다. L2에만 제곱을 하는 이유는 기울기가 단순해지는 효과가 있기 때문이다.

L2 loss는 classifier 계열의 loss보다 최적화하기가 훨씬 어렵다는 점에 유의해야 한다. L2 loss는 요구되는 정확한 출력을 요구하는데 비해, Softmax는 상대적이 비율로 값보단 크기를 고려하기 때문이다.또한 L2 loss가 outlier로 발생한 과도한 기울기에 취약하다.
이에 회귀 문제는 출력을 일정 구간의 그룹으로 나눌 수 있는지 고민해봐야한다. 예시로 1~5 점을 예측하는 문제에 절대적인 점수보다, [1,2,3,4,5]의 클래스로 두고 예측하는 것이 성능이 좋다. 또한 이러한 방식은 regression outputs([1,2,3,4,5] 별 Softmax 값)에 대한 분포도 확인 가능하다.
Reference
CS231n 강의 노트 링크 : https://cs231n.github.io/neural-networks-2/
'딥러닝 > Basic (CS231n)' 카테고리의 다른 글
| [CNN] Optimizer (Momentum, Nesterov, RMSprop, Adam...), Hyperparameter tuning, Evaluation (0) | 2024.06.01 |
|---|---|
| [CNN] Gradient check, 모델 학습 지표 (0) | 2024.05.25 |
| [CNN] Neural Network(신경망), Neuron (뉴런), Activation function(활성화 함수) (0) | 2024.05.11 |
| [CNN] Backpropagation(역전파), chain rule (0) | 2024.05.04 |
| [CNN] Optimization (최적화), Gradient(기울기 계산), Learning rate (0) | 2024.04.27 |