
Neural Network (신경망)
linear classification는 시각적 정보를 score = W (가중치) * x (입력)를 통해 각 클래스 별 점수로 계산한다. Neural network(신경망)는 여러 개의 linear classifier를 각각의 layer로 구성되며, 아래는 2개의 layer 예시이다.

첫 번째 식에서 W1의 크기가 [100 x 3072], W2의 크기는 [10 x 100] 와 같이 임의로 설정하며, 최종적으론 linear classifier와 동일하게 10개의 클래스에 대한 점수를 계산한다. 또한 사이에 들어가는 max 함수는 비선형성을 구현하는 기능을 한다. 만약 이 비선형성이 없으면 기존의 linear classifier와 같은 선형 험수로 단순화 될 수 있다. 이렇게 얻은 식에서 각 파라미터 W1, W2는 SGD를 통해 학습되며, 각각의 기울기는 chain rule로 backpropagation 된다.
Neruon (뉴런)
신경망은 사실 생물학적 신경 시스템을 모델링하는 것을 목표, 다만 기계 학습으로 파생되어 좋은 결과를 얻다. 기계 학습에서 영감을 받은 생물학적 시스템은 뇌의 기본 계산 단위인 뉴런이다.
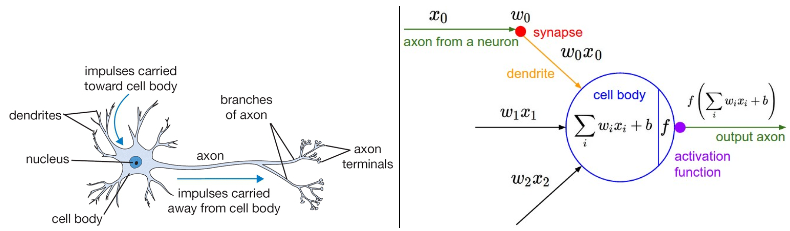
각 뉴런은 자신의 수상 돌기(dendrites)에서 입력을 받아들이고, 축삭 돌기(axon)를 통해 출력을 내보낸다. 축삭 돌기는 이후 여러 갈래로 분기되어 서로 다른 뉴런의 수상 돌기에 시냅스(synapse)를 통해 연결된다. 이를 수학적 뉴런 구조 이미지에서 수학적으로 이해할 수 있다.
축삭 돌기를 따라 이동한 신호(x0)는 시냅스 강도(w0)에 곱(w0 * x0)으로 상호작용한다. 여기서 시냅스 강도(w)는 학습 가능하며, 이전 뉴런이 다음 뉴런에게 미치는 영향의 강도(크기)와 방향(±)을 제어한다. 기본적으로 세포체(cell body)에서는 모든 신호를 합산한다. 최종 합이 임계값(threshold)를 초과 (ReLU를 가정) 하면 축삭 돌기로 출력을 내보낸다. 합산 후의 신호 강도를 0~ 1 사이의 범위로 압축하여 출력을 내보내는 시그모이드 함수 σ 도 f로 사용 가능하다.
다시 말해, 각 뉴런은 입력과 가중치의 내적을 수행하고 편향을 더하며 비선형성(또는 활성화 함수)을 적용한다. 참고로 기계 학습 뉴런 모델에 비해 생물학적 뉴런 모델은 훨씬 복잡하다. 뉴런의 구조는 모두 동일하지만, 단순하지 않고 시냅스는 단순한 가중치 구조이지 않으며 축삭 돌기로 값을 단순히 출력하는 것 외에 정확한 타이밍에 값을 출력해야하는 문제도 생물학적 뉴런 모델은 포함하고 있다.
Linear classifier로 동작하는 뉴런
뉴런은 다수의 입력 중 일부을 "선호"(활성화가 1에 가까운)나 "비선호"(활성화가 0에 가까운)로 출력 할 수 있다. 여기에 적절한 loss function을 사용하면 linear classifier로 활용 가능하다.
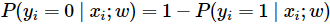
Binary Softmax classifier의 정답이 >둘 중 하나이기 때문에, 두 확률의 합이 1이며 클래스 별 확률은 위와 같다. 시그모이드 함수를 활성화 함수로 사용시 0~1까지 출력이 제한되기 때문에, 0.5보다 큰지 여부로 예측할 수 있다. 이를 최적화하기 위해 cross-entropy loss를 사용한다.
Binary SVM classifier 는 최대 마진 hinge loss를 사용하면 Binary SVM classifier로 훈련된다. 두 종류의 classifier 모두 regularization loss를 포함하고 있다.
Regularization은 생물학적 시간이 지남 따라 서서히 잊는 것으로 해석할 수 있다. 이유는 Regularization 의 존재로 가중치 w가 학습을 반복할수록 0으로 수렴하기 때문이다.
Activation function (활성화 함수)
Activation function(활성화 함수)는 단일 숫자를 가져와 고정된 연산을 수행하는 함수다.
Sigmoid
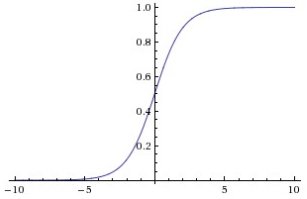
실수 값 숫자를 가져와 0과 1 사이의 범위로 "압축". 특히, 큰 음수 값은 0이 되고 큰 양수 값은 1이 된다. 0이면 동작 X, 1이면 최대치로 동작중 뉴런의 동작율 (firing rate)로 해석하는 경우도 있다. 다만 두 가지 단점으로 최근에는 많이 사용되지 않는다. 그 이유는 아래와 같다.
- Gradient vanishing(기울기 소멸). 뉴런이 0 또는 1로 극단적으로 saturation 되는 경우다. 기울기가 0이 되어버리며 이는 최종 출력이 입력까지 backpropagation 되는 중 기울기가 흐르지 않게 되는 상황을 초래한다. -10 or 10만 되어도 거의 0,1 수준의 값이 나오는데, 이에 초기 가중치가 매우 크다면 ±10 의 범위를 초과하기 쉽고, 학습이 진행되지 않는다.
- 시그모이드를 통과한 출력의 중심치가 0이 아님. Gradient vanishing 만큼 심각한 문제는 아니다. "f = w*x + b"의 뉴런으로 들어오는 데이터가 항상 양수인 경우, 가중치 w 에 대한 기울기는 역전파 중 모두 양수 혹은 음수가 될 것이다. 이것은 가중치 업데이트 중 불필요한 지그재그 동작을 유발하나, 배치를 통해 기울기를 합산하면 w 최종 업데이트에 대한 부호가 정해지므로 문제가 완화된다.
Tanh

실수 값을 [-1, 1] 범위로 "압축"한다. 시그모이드와 마찬가지로 활성화가 saturate되지만 (-1 혹은 1로 수렴), 시그모이드과 달리 출력이 중심이 0이다 단순히 스케일된 시그모이드 뉴런으로 볼 수 있으며 "tanh(x)=2σ(2x)−1" 가 성립한다.
ReLU (Rectified Linear Unit)
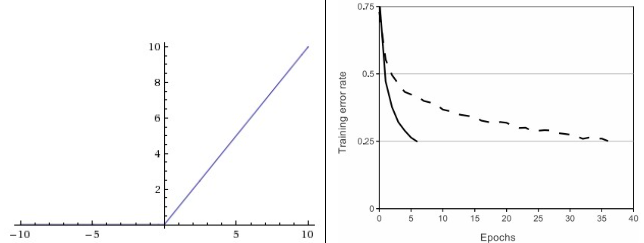
가장 많이 사용되는 activation function 중 하나다. f(x)=max(0,x) 로 표현. 0 을 임계값으로 둔 활성화 함수다. Sigmoid, Tanh와 비교하여 SGD의 수렴을 크게 가속화한다. 그 이유는 ReLU의 선형성과, 포화되지 않는 특징 때문이다. 또한연산량이 큰 지수 함수가 포함된 Sigmoid, Tanh 대비 단순히 임계값을 지정함으로 비선형성을 간단하게 구현한다.
ReLU 유닛은 훈련 중에 무너지거나 "죽을" 수 있다. 이는 아무리 큰 기울기가 ReLU를 통해 흘러도 기울기가 특정 지점에서는 사용되지 않을 수 있다. 또한 그 이후의 기울기는 영원히 0이 된다. 예시로 Learning rate가 너무 높게 설정되었을때 발생, 이 경우 활성화 되지 않는 뉴런이 전체의 40%를 차지하기도 한다. 이에 적절한 학습률에 대한 검증이 필요하다.
Leaky ReLU
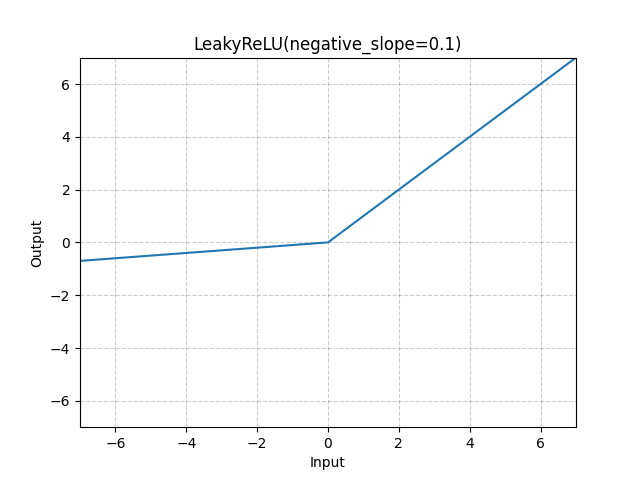
Leaky ReLU는 ReLU가 "죽는" 문제를 해결하기 위한 시도다. x < 0 일 때 0이 아니라 작은 기울기(a)를 준다. 다만 성능이 일관되지 못하며, PReLU라는 a를 파라미터로써 학습하는 방법도 존재한다.
Maxout
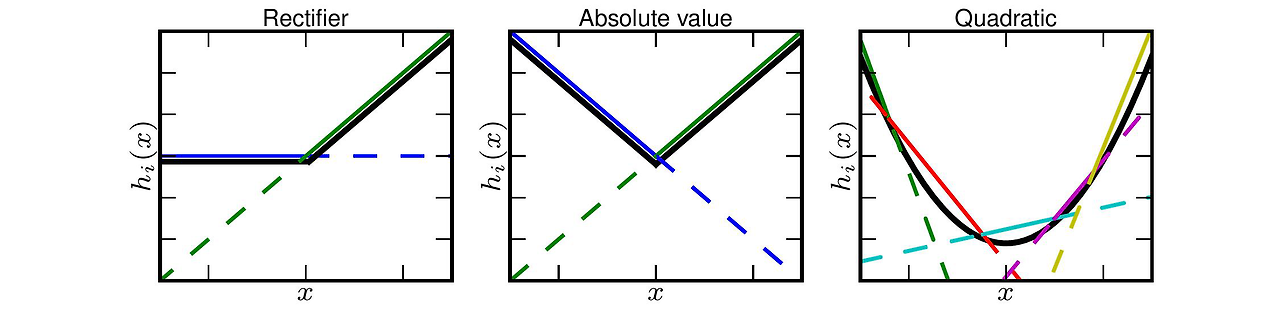
Output에 비선형을 부여하는 지금까지의 일반적인 activation function 과는 다른 형태다. 많은 function이 있고 Maxout이 대표적이다. ReLU를 일반화 한 방식이며, 0이 아닌 score 중 에서 max값을 취한다.
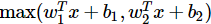
ReLU (Leaky ReLU 포함)는 이 형태의 한 경우로 (w1, b = 0 인 경우) 볼 수 있다. Maxout은 지수 함수 없이 saturate 되지 않으면서, "죽는" unit 이 없는 장점이 있으나, 파라미터가 매우 많아지는 문제가 존재한다.
결론적으로, ReLU를 시도하고 "죽는" 유닛이 많다면 Leaky ReLU 또는 Maxout을 시도하는 것이 기초적인 방법이다. Sigmoid는 최악의 방법으로 볼 수 있으며, Tanh는 시도해볼만 하나 좋은 성과가 없을 것이다. 추가로 한 네트워크에 서로 다른 activation function을 혼합하여 연결하는 것은 드물긴하나, 문제가 되지는 않는다.
신경망의 구조
신경망은 비순환 그래프로 연결된 뉴런들의 모음으로 모델링된다. 즉, 일부 뉴런의 출력은 다른 뉴런의 입력이 되며 무한 loop을 방지하기 위해 입출력이 순환하지 않는다. 또한 신경망은 layer내 뉴런들을 하나씩 개별로 구분할 수 있다. 기본적인 layer 구조에는, 두 인접한 layer 간 모든 뉴런이 쌍으로 연결된 fully-connected layer가 있다. FC layer에서 동일 layer내의 뉴런끼리는 연결되지 않는다.
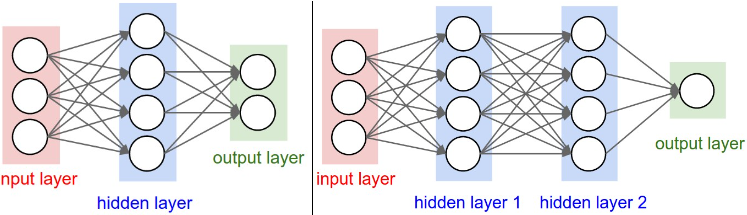
N-layer 신경망이라고 말할 때 input layer은 계산에 포함되지 않는다. 만약 input - output으로만 이어지면 1-layer가 된다. SVM이나 logistic regression은 이런 관점에서 1-layer 신경망의 특별한 케이스다.
위 이미지와 같은 구조를 “Artificial Neural Networks” (ANN) 혹은 “Multi-Layer Perceptrons” (MLP) 라고도 부른다. Output layer는 activation function이 적용되지 않는다. 이는 output layer가 주로 점수, 확률, 원하는 output(회귀의 경우) 등 실질적으로 사용되는 숫자이기 때문이다. 신경망의 크기는 뉴런의 수 or 파라미터의 수로 측정한다. 위 이미지의 2-layer 신경망을 예시로 뉴런은 6개 / 파라미터는 3*4 + 4*2 = 20 의 w / 4+2 = 6의 b로 26개의 파리미터 수를 가지고 있다.
Feed-forward 연산
신경망이 layer로 구성되는 주요 이유 중 하나는 이 구조가 행렬-벡터 연산을 사용하여 학습하는 것을 매우 간단하고 효율적으로 만들기 때문이다. 이전 이미지의 3-layer 신경망을 예시로 들면, input = [3x1] / W1 = [4x3] / b1 = [4x1] .... 의 크기를 가지는 행렬로 표현된다. 이를 np.dot(w,x) 을 통해 입력과 가중치를 한번에 곱해줄 수 있다. 따라서 3-layer 신경만은 세번의 행렬 곱 및 2번의 활성화 함수로 구성된다.
# 3-layer 신경망의 forward-pass :
f = lambda x: 1.0/(1.0 + np.exp(-x)) # activation function (sigmoid)
x = np.random.randn(3, 1) # input vector (3x1)
h1 = f(np.dot(W1, x) + b1) # 1st hidden layer + activations (4x1)
h2 = f(np.dot(W2, h1) + b2) # 2nd hidden layer + activations (4x1)
out = np.dot(W3, h2) + b3 # output vector (1x1)위 코드에서 W1, W2, W3, b1, b2, b3는 네트워크의 학습 가능한 파라미터이다. 또한 x에 [nx1]의 vector가 아닌, [n x batch]를 입력함으로써 여러 예제를 효율적으로 병럴적으로 계산할 수 있다. 이전에서 언급한 것과 같이 최종 out layer는 activation function이 적용되지 않는다.
Representational Power
Fully-connected layer로 구성된 신경망은 가중치로 이루어진 함수 집합으로 볼 수 있다. 함수 집합은 무엇을 의미하며 어디까지 표현될 수 있는가?(representational power) 적어도 하나의 hidden layer를 가지는 신경망은 존재하는 모든(universal) 함수에 근사할 수 있다.
그렇다면 왜 여러개의 layer를 쌓아 더욱 깊게 들어가야하는가? 신경망이 실제로 잘 작동하는 이유는 데이터의 통계적 특성과 잘 맞는 부드러운 함수를 간결하게 표현하기 때문이다. 또한 최적화 알고리즘(예: 경사하강법)을 사용하여 쉽게 학습된다. 1개의 hidden layer 신경망과 여러개의 hidden layer의 신경망의 representatinal power는 동일하다고 볼 수 있으나, 깊은 신경망이 좋은 성능을 보이는 건 경험을 통해 확인됨된다.
또한 3개보다 더 깊은 4,5,6,... 개 로 layer가 늘어나면 성능의 개선되는 폭은 작아진다. 다만 CNN에서는 더욱 깊을 수록 성능이 좋다고 밝혀졌으며 서로 반대되는 이야기인데, CNN에서 다루는 이미지 데이터는 hierarchical (계층적)인 구조로 이루어져있기에 성능이 좋아진다고 예상된다.
Layer의 수 및 크기 설정
layer의 수 및 layer 별 크기는 어떻게 정해야할까? 먼저, 신경망의 크기와 층의 수를 증가시키면 신경망의 "용량"이 증가한다는 것을 유념하자. 즉, 뉴런들이 다양한 함수를 표현할 수 있는 공간이 증가한다.

이에 대한 예시 (이진 분류) 는 위와 같으며, 더 큰 신경망은 더 복잡한 함수를 나타낼 수 있다. 하지만 깊은 layer는 양날의 검. 더 복잡한 데이터를 분류 할 수 있지만, Overfitting(과적합)을 유발할 수 있디. Overfitting 이란 "용량"이 높은 모델에서 데이터의 노이즈까지 훈련하여 이를 포함하여 "fit"(예측)하는 현상이다.
위 예시에서 hidden layer가 적을 수록 노이즈에 overfit 되지 않고 generalization(일반화)가 잘 된 것을 볼 수 있다. 20 hidden layer 모델은 정답을 전부 맞추긴 하지만, 너무 많이 영역이 분리되었고 노이즈를 인지하지 못한다.
다만, 데이터가 과적합을 방지할 만큼 복잡하지 않다면 더 작은 신경망이 좋다고 오해할 수 있다. Layer 수를 줄이기보단, 깊은 layer에 제약 조건을 추가하는 것이 더 좋은 방법 (L2 regularization, 드롭아웃 등) 그 이유는 작은 신경망이 경사 하강법과 같은 방법으로 훈련하기가 더 어렵기 때문이다.
Layer가 적을 수록 loss function의 minima가 상대적으며(local minima가 적고 수렴하기 쉬운 장점은 있음), 또한 동일 모델을 여러번 학습했을때, 적은 layer로 구성된 모델의 최종 loss가 분산이 훨씬 크다는 것도 불리한 방향이다.이는 곧 layer가 깊을 수록; 모든 학습에 거의 동일하게 성능이 좋으며, 랜덤 초기화에 덜 의존적으로 볼 수 있다.

따라서, layer의 수보다 regularization strength가 overfitting을 제어하는데 좋은 방법이다. 위 이미지는 모두 똑같은 20개의 hidden layer로 이루어져 있으나, regularization에 따라 영역의 형태가 달라진다. 결론적으로, 구현할 수 있는 최대의 연산량을 갖춘 모델에 여러 regularization을 추가하는 것이 좋은 방향이다.
Reference
CS231n 강의 노트 : https://cs231n.github.io/neural-networks-1/
'딥러닝 > Basic (CS231n)' 카테고리의 다른 글
| [CNN] Gradient check, 모델 학습 지표 (0) | 2024.05.25 |
|---|---|
| [CNN] Preprocessing (전처리), Weight init (가중치 초기화), Loss function (손실 함수) (0) | 2024.05.18 |
| [CNN] Backpropagation(역전파), chain rule (0) | 2024.05.04 |
| [CNN] Optimization (최적화), Gradient(기울기 계산), Learning rate (0) | 2024.04.27 |
| [CNN] Linear classification (SVM, Softmax) (2) | 2024.04.20 |