
Gradient Check
Gradient check은 기울기를 직접 확인하는 것으로 복잡하고 오류가 종종 발생한다. 관련된 문제 및 팁은 아래와 같다.
중심치(centered formula)를 사용

h는 매우 작은 수로, 실제로는 대략 1e-5 정도ek. 각 차원의 기울기를 확인하기 위해 loss function을 두 번 계산해야한다. 따라서 비용이 약 2배 정도 더 사용되나, 기울기는 훨씬 더 정확해진다.
상대 오차(relative error)를 사용하여 비교

직접 수식을 구한 f'a(analyic gradient)와 근사를 사용하는 f'n(numerical gradient)의 동일성을 판단할때 사용하는 방식이다. 차이가 단순히 특정 임계값(threshold)를 넘었다는 것으로 동일 하지 않다고 판단할 수 있을까? 예를 들어, 차이가 1e-4인 경우에두 기울기가 모두 1.0 정도인 경우에는 적절한 차이처럼 보이며 두 기울기가 1e-5 또는 그 이하인 경우에는 1e-4가 엄청난 차이로 실패로 간주된다. 따라서 임계값의 설정은 무의미하다.
따라서 상대 오차를 고려해야한다.|f'a - f'n| 로 표현된 차이의 절대값과 각 기울의 절대값 중 큰 하나로 나누어 계산한다. 절대값은 0으로 나뉘는 것을 방지하기 위함이다. 또한 두 기울기가 모두 0인 경우에 대해 항상 신경써야 한다. 일반적으로 1e-7 이하면 good, 1e-2 이상이면 bad로 판단된다. 그 사이는 어떤 loss function을 사용 했는지, network의 깊이에 따라 좋고 나쁨을 고민해야 봐야한다.
Double precision을 사용
32비트의 single precision 보다 64비트의 double precision은 더 구체적으로 값을 표현함으로서 상대 오차를 획기적으로 줄인다. (표현할 수 있는 숫자의 크기 차이) 추가로 소수점의 범위를 이상적인 수준으로 유지한다. 일반적으로 신경망은 batch 구성 형태로 loss function을 구하고 normalize 한다. 하지만 각각의 기울기가 너무 작으면 나눗셈을 취하는 과정에서 수가 너무 작아지는 문제를 야기한다. 이에 절대적인 loss의 값이 "더 나은" 범위를 가지는 값이 되게 조절하는 것이 필요하다.
Kink를 고려

Kink는 기울기의 오차를 유발하는 하나의 원인. 이는 ReLU, SVM, Maxout 등에서 미분이 불가능한 지점을 의미한다. 오차는 위 ReLU 예시에서 x가 0에 극단적으로 가까울때 여전히 기울기는 0이지만, h로 인해 기울기가 발생할 수 있다. 실제로 굉장히 많은 비선형 함수가 사용되기 때문에 생각보다 흔한 경우다. f(x+h)와 f(x−h)에서 max 연산을 취해, 선택된 값이 두 f에서 다르다면 kink의 영향이 발생했다고 볼 수 있다.
적은 Gradient check 포인트만 사용
이는 Kink를 해결하기 위함으로, 절대적은 수를 줄여 영향을 줄이는 것이다. 또한 적으면 적을수록 속도적인 측면에서 유리하며 2~3개의 point로 전체 배치에 대해 check를 수행 할 수 있다.
h의 크기에 대한 주의

작다고 무조건 좋지는 않음. h가 작으면 더 정확해질 순 있으나, 소숫점 연산의 측면에서 오류가 발생할 수도 있다.
"Characteristic"한 지점에서 기울기를 확인
Gradient check은 전체 공간 중 임의의 한 지점에서 이루어진다. 다만 해당 지점의 기울기가 globally하게 전파되는 유의미하고 정확한 값인지는 알 수 없다. 이를 보안하기 위해 짧은 burn-in (초기화) 시간 후에 gradient check 를 수행함으로써 모든 지점이 어느 정도 일반화 되었다는 가정으로 유의미하다는 판단을 할 수 있다. "characteristc"을 찾기 보다는, 모두 동일한 "characteristic"을 지닌 상황에서 기울기를 확인하는 방향이다.
지나친 regularization을 주의
Loss function 에 regularization loss은 반드시 필요하다고 이전에 언급했다. Regularization loss가 data loss보다 비중이 크면 data loss에 대한 해석이 불가능할 수 있다. Data loss와 Regularization loss를 개별로 확인하여 따로 해석하는 방법을 이용한다. λ (regularization strength)로 Regularization loss를 극단적으로 키우면, data loss 없는 상황을 구현할 수 있다.
Dropout과 augmentation 없이 검토
직접적인 기울기를 확인할 때, 랜덤한 요소가 추가되면 실제 기울기와 다른 값을 계산하게 된다. 이러한 효과를 함께 검토하기 위해선 특정 random seed를 고정한 뒤에 gradient check를 수행하면 된다.
일부 차원만 검토
기울기는 수백만 개의 파라미터를 가질 수 있다. 이러한 경우 기울기의 일부 차원만 확인하고 나머지는 올바르다고 가정하는 것이 현실적이다. 다만 일부 차원을 확인하는 것이지, 일부 파라미터만을 확인하는 것은 아니다.
학습전 기본적인 Tips/Tricks
- 올바른 loss 선정 및 모델을 구현하고 적정한 값이 나오는지 확인. CIFAR-10을 예시로 초기화된 가중치를 사용하여 Softmax loss를 구하면, 10개의 클래스 별 확률은 0.1이 될 것이고 loss는 -ln(0.1) = 2.302가 나와야한다. SVM의 경우 모든 점수가 0이 나오고, 마진이 1일 경우 loss는 9가 된다.
- 적절한 λ(regularization strength) 선정으로 loss를 적당히 증가시켜야한다.
- 일부 sample을 활용한 overfit(과적합) 유발. 데이터의 아주 작은 부분(ex : 20개의 sample)에 대해 학습하고 손실이 0이 되는지 확인하는 것이다. ( λ = 0)0을 확인하지 못하면 전체 dataset을 진행할 가치가 없다. 또한 0으로 overfit된다 해도, 전체 dataset이 무조건 일반화된다는 가정은 잘못됐다.
여러 모델 학습 지표
훈련 과정에서 모니터링해야 할 유용한 여러 가지 지표가 있으며, 이는 하이퍼파라미터 설정에 대한 판단과 효율적인 학습을 위한 조치사항을 검토할 수 있다.Dataset의 반복 횟수인 iteration과 각 sample의 진행 횟수인 epoch 중, Epoch을 모니터링에 활용하는 것이 이상적이다.
Loss function

Epoch 별 매번 계산된다. 낮은 learning rate에서 loss는 선형적으로 나타나며, 매우 높은 learning rate에서는 지수 함수처럼 보인다.적당히 높은 learning rate는 더 적절한 값을 찾아가지 못하고 특정 영역에 갇히게 된다.
오른쪽은 CIFAR-10을 학습시킨 신경망의 loss chart 예시다.Loss가 감소하면서 진동이 발생하는 것은 batch size가 작다고 의심해볼 수 있다. 전체 dataset으로 1개의 batch만 학습한다고 하면, 흔들림이 발생하지 않는다. (매번 동일한 data라서 같은 방향을 가짐) 적절한 learning rate는 지수 함수의 형태를 띄고 있어 log plot으로 그려도 모니터링하기 좋을 수 있다.
Train/Val accuarcy
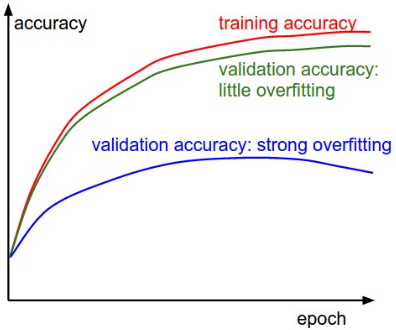
Accuracy(정확도)도 중요한 지표 중 하나다. 이는 모델의 overfit(과적합)을 판단하기 유용하다. Training 과 Validation 간 정확도 차이는 overfit의 정도로 해석 가능하다.
차이가 클수록 overift이 과해진다고 해석 할 수 있다. Overfit은 regularizataion 강화하거나, 더 많은 sample을 사용함으로써 개선할 수 있다. 다만 차이가 매우 적다고 판단되면, 파라미터를 늘려야할 필요가 있다. 엄연히 data가 다른데 결과가 동일하다는 것은 모델이 설명할 수 있는 "용량"(capacity)이 부족하다는 의미한다.
Ratio of weights:updates
실제 가중치의 값에 대한 변동치의 비율에 대한 비율도 활용 가능하다. (learning rate까지 곱하진 최종 변동치를 기준) 대략 1e-3 정도가 적당하며, 이를 기준으로 높거나 낮으면 learning rate을 조정해야 한다 판단 가능하다.이 과정에서 가중치의 비율 중 최대, 최소보단 norm 값을 주로 사용한다.
Activation / Gradient distributions per layer
각 레이어의 activation / gradient 히스토그램을 확인하여, 가중치의 분포가 적절한지 확인해야한다. 특히 처음 초기화되었을때 좋지 않은 분포는 학습을 느리거나 중단시켜버릴 수 있다. 예시로 tanh의 뉴런이 [-1,1]에 골고루 분포된 출력이 아닌, 전부 0이거나, -1 혹은 1로 전부 포화되버린 상태인지 확인한다.
First-layer Visualizations

특히 이미지 data를 다룰 때, 첫 레이어를 시각화 하는것이 도움이 될 수 있음다. 위예시 중 왼쪽은 노이즈가 확실히 많아보이며 정확한 원인은 모르나 어딘가 문제가 있다는 의미한다. 오른쪽은 왼쪽에 비에 노이즈 없이 뚜렷하다.
Reference
CS231n 강의 노트 : https://cs231n.github.io/neural-networks-3/