
Backpropagation (역전파)
Backpropagation은 chain rule을 이용하여 기울기를 계산하는 방법이다. 신경망의 이해, 설계, 디버깅의 핵심이다. 입력 x와 함수 f가 주어졌을때, x에 대한 f의 기울기 계산이 목표다. 하지만 기울기는 x에 대해 한 번에 계산되지 않고, 각 weights 에 대한 기울기를 따로 계산하며 loss에 가까운 weight 부터 순서대로(chain) 업데이트를 수행한다. 또한 training data를 포함한 전체 기울기 또한 신경망의 시각화 및 해석에 유용한 경우도 있다.
표현식 및 기울기의 해석

임의의 f(x)에 대한 편미분은 특정 지점 근처의 무한히 작은 영역에서 함수의 변화율을 나타낸다. h가 아주 작을 때 (0으로 수렴), 함수는 직선으로 근사되고, 그때의 기울기가 도함수 값이 된다.

또한 위 식과 같이 x가 h만큼 변화한 경우, x에 대한 편미분에 h를 곱한 만큼 값이 변화되었다고 볼 수 있다.

곱셈 함수에서 각 입력에 대한 편미분을 유도하는 것은 간단한 미적분 문제다. 곱셈 함수에서 도함수는 변수 x,y,.... 들의 민감도(sensitivity)라고도 볼 수 있다. 단순 f(x,y) = xy 에서 x에 대한 편미분은 y이고, x의 변화에 따라 y 만큼 "민감"하게 값이 변화하기 때문이다.

덧셈 연산에 대한 도함수도 유도 가능하다. x, y에 대한 도함수는 x,y의 값이 무엇이든지 상관없이 1이다. 이는 x 또는 y 중 하나를 증가시키면 f의 출력이 증가한다 또한 곱셈의 경우와는 달리 x, y의 실제 값과는 관계가 없다. 그 이유는 도함수에 x, y항이 남아있지 않기 때문이다.

마지막은 max 함수에 대한 도함수이다. 입력 중 큰 변수에 대해 1이고 다른 입력에 대해선 0이다. 예시로 입력이 x=4, y=2인 경우, 최댓값은 4(x)이고 함수는 y 값에 대한 영향은 없다. 즉, y를 아주 작은 h만큼 증가시켜도 함수는 계속 4를 출력하고, 따라서 기울기는 0이다. 만약 y를 2보다 크게 변화시킨다면 f가 바뀌나, 기본적으로 도함수는 작은 변화에만 유효하기에 큰 의미는 없다.
Chain rule
f(x,y,z)=(x+y)*z 와 같은 합성 함수에서 한다. 직접 편미분을 구할 수 있는 수준의 함수이나, Chain rule을 위한 예시다. 이 식은 두 개로 나누어 표현할 수 있다. (q=x+y, f=q*z) 이 후 두 개의 식은 각각 별도로 편미분이 가능하다.

q에 대한 기울기는 중요하지 않고, loss function이 될 f에 대한 x,y,z 별 기울기가 중요하다. Chain rule은 도함수들을 곱셈을 통해 "chain"시키는 방법이다. x에 대한 f의 기울기를 구하면 아래와 같으며, 위 에서 구한 q에 대한 편미분 결과에서 그 값을 구할 수 있다.

다른 y,z도 동일한 방식으로 기울기를 구할 수 있다. 이러한 방식으로 함수 기울기를 구하는 것이, chain rule을 활용한 backpropagation이다.
Backpropagation의 이해
역전파(backpropagation)는 local process이다. 함수 전체가 아닌 특정 local에서 진행되는 방식이라는 의미이다. 특히 각 게이트는 전체를 고려할 필요 없이 완전히 독립적으로 이를 수행한다.

forward pass 는 입력부터 최종 출력까지 계산한다 (초록). 이 과정에서 각 게이트(local)는 입력을 받을때 1) 출력값 2) 입력에 대한 출력의 local gradient를 둘 다 계산한다. bacward pass 는 최종 output에서 시작하여 chain rule을 활용해 input까지 기울기를 전파한다.(빨강) Backpropagation은 최종 출력을 활용하여 이미 계산된 local gradient를 통해 학습하게 된다. 즉 chain rule을 통해 최종 output 부터 input 까지 각 게이트는 스스로 기울기를 계산하게 된다.
위 이미지에서 덧셈 게이트는 입력 [-2, 5]를 받아서 3을 출력하며 각 입력에 대한 local 기울기는 +1이다. (입력 별 도함수) 이후 곱셈 게이트로 최종 값 -12를 얻는다. 또한 여기서 최종 출력에 대한 덧셈 게이트의 기울기는 -4이다. (입력 별 도함수) 최종 output의 gradient 값이 1이라고 가정하자. output에 대한 덧셈 게이트의 기울기는 -4다. (chain rule) 덧셈 게이트에 대한 x,y의 기울기는 1이므로, 1 * -4 = -4 로 최종 출력에 대한 x,y의 기울기도 -4가 된다. (chain rule)
이에 최종 출력(-12)을 높이고 싶다면, 도함수가 -4이기 때문에 덧셈 게이트는 낮추는 방향(음수)으로 변동해야 한다. 같은 가정하에 x,y 도 낮아지는 방향으로 4에 비례한 만큼 변동해야 한다. 이는 덧셈 게이트가 낮추는 방향인 이유와 동일하다
Chain rule with Sigmoid
어떤 종류 함수여도 미분 가능하면 게이트로 작용할 수 있으며, 여러 개의 게이트를 하나의 게이트로 합치거나 하나의 게이트를 편의를 위해 여러개로 나눌 수 있다.


위 식은 2d 입력에 대한 sigmoid activation (시그모이드 활성화) 함수이다. f(w,x)는 여러 개의 게이트로 구성되어 있으며, 4가지 도함수 이용하여 이 식을 chain rule 로 표현 가능하다. 특히 c, a 는 입력을 상수 값으로 변환한 것으로, 변환된 입력의 기울기는 필요하지 않은 경우에 활용할 수 있다. 예를 들어, w0x0 + w1x1에 대한 x1의 기울기가 필요하면 x0는 상수 취급해도 상관 없다.

회로 형식으로 시그모이드 함수를 시각화한 예시이다. 입력 x와 가중치 w의 스칼라 곱 (dot product)을 기반한 함수의 연속체이다. 입력은 [x0,x1], 가중치는 [w0,w1,w2] (w2는 bias). 최종 출력은 [0, 1] 사이의 임의의 실수이다. (시그모이드 함수 특징) σ(x) 로 표현된 시그모이드 함수의 도함수는 아래와 같다.
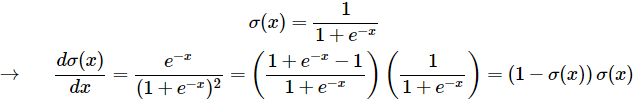
기울기는(1 - σ(x)) * σ(x)로 매우 단순하게 정리가 된다.위 회로를 기준으로 입력 1.0을 받으면 출력은 0.73 이며 기울기는 (1 - 0.73) * 0.73 ≈ 0.2 이다. 여기서 입력은 x, w에 대한 계산을 한 값. x를 의미하는 것이 아니다. 이를 통해 여러 연산을 단일 게이트로 그룹화하는 것이 매우 유용할 수 있다. (*-1, exp, +1 등을 σ(x) 하나로 묶음)
또한 역전파를 쉽게 수행될 수 있게 forward pass를 여러 단계로 나누는 것이 도움이 될 수 있다. 예시로 x, w에 대한 dot product을 곱셈과, 덧셈으로 나누었다. 결국 핵심은 역전파가 어떻게 수행되는지, forward pass의 어떤 부분을 게이트로 활용할지에 따라 효율이 달라진다. 최소한의 코드와 연산으로 chain을 형성하는 방법을 고민해봐야 함.
Python Code 예시

위 식의 backpropagation 을 Python code로 구현한 예시다. (σ(x)는 sigmoid) 식을 그대로 x,y에 대한 기울기를 계산하려면 굉장히 길고 복잡한 수식을 구해야한다. 하지만 forward, backward pass를 이용하면, 복잡한 수식을 구할 필요가 없다.
x, y = 3, -4 # 예시
# forward pass
sigy = 1.0 / (1 + math.exp(-y)) # 분자 (1)
num = x + sigy # 분자 (2)
sigx = 1.0 / (1 + math.exp(-x)) # 분모 (3)
xpy = x + y # 분모 (4)
xpysqr = xpy**2 # 분모 (5)
den = sigx + xpysqr # 분모 (6)
invden = 1.0 / den # 분모 (7)
f = num * invden # 전체 (8)전체 수식을 여러 게이트로 구조화하여, 각각의 변수에 대한 기울기를 계산할 수 있도록 한다. 역전파에서 각 변수들은 (sigy, num, sigx, xpy, xpysqr, den, invden) 회로의 출력에 대해 기울기를 계산하게 된다. 역전파에서 모든 영역은 각 표현식의 기울기를 계산. 이를 기울기에 대한 곱셈으로 chain을 형성한다.
# backprop f = num * invden
dnum = invden #(8)
dinvden = num #(8)
# backprop invden = 1.0 / den
dden = (-1.0 / (den**2)) * dinvden #(7)
# backprop den = sigx + xpysqr
dsigx = (1) * dden #(6)
dxpysqr = (1) * dden #(6)
# backprop xpysqr = xpy**2
dxpy = (2 * xpy) * dxpysqr #(5)
# backprop xpy = x + y
dx = (1) * dxpy #(4)
dy = (1) * dxpy #(4)
# backprop sigx = 1.0 / (1 + math.exp(-x))
dx += ((1 - sigx) * sigx) * dsigx #(3)
# backprop num = x + sigy
dx += (1) * dnum #(2)
dsigy = (1) * dnum #(2)
# backprop sigy = 1.0 / (1 + math.exp(-y))
dy += ((1 - sigy) * sigy) * dsigy #(1)역전파를 계산하기 위해 forward pass 에서 사용된 일부 변수를 가지고 있는 것이 매우 도움이 된다. 이는 Cache 생성한다고 볼 수 있다. 그렇지 않다면, 역전파 중에 forward pass를 계산해야되는 연산량 loss가 발생한다. 그리고 변수 x, y는 forward pass에서 계신된 각 게이트 별 기울기 식에 여러번 사용된다. 이에 해당 변수에 대한 기울기는 "=" 아닌 "+=" 로 누적해야 한다. 이는 여러 부분으로 분기되며 흐르는 기울기를 전부 고려할 수 있게 한다.
Backward flow의 해석
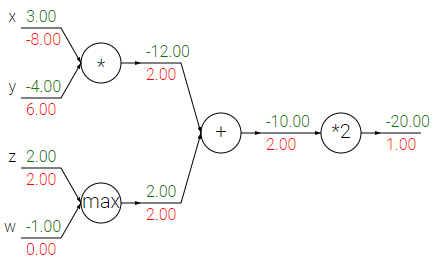
가장 일반적으로 사용되는 세 가지 게이트 (덧셈, 곱셈, 최댓값)의 해석은 아래와 같다.
- 덧셈 게이트 : 출력의 기울기를 가져와 입력이 어떤 값인지 고려하지 않고, 모든 입력에 동일하게 라우팅한다. Local gradient가 +1.0 이기 때문에 모든 입력의 기울기가 정확히 출력의 기울기와 같게 된다.
- 최댓값 게이트 : 덧셈 게이트와는 달리 기울기를 정확히 하나의 입력에만 라우팅한다. (입력이 큰 값으로) 덧셈 게이트와 동일한 점은 기울기의 변화는 없다. 높은 값에 대한 local gradient는 1.0, 작은 값은 0.0 이기 때문이다.
- 곱셈 게이트 : 상대적으로 직관적이지 않다. local gradient는 다른 입력값, 기울기는 여기에 출력의 기울기를 곱한 값이다. 위 예시에서 x에 대한 기울기는 -4 (다른 입력 y의 값) * 2 (출력의 기울기) = -8 이다.
만약 곱셈 게이트 중 하나의 입력이 매우 작고 다른 하나가 매우 크다면, 작은 입력에는 상당히 큰 그래디언트를 할당하고 큰 입력에는 아주 작은 그래디언트를 할당한다. 이는 자신이 아닌 다른 입력값을 local gradient로 가지기 때문이다. 이에 입력 x와 가중치 w이 곱셈 연산이 취해지는 linear classifier의 경우, 입력의 크기가 기울기의 크기에 영향을 미친다. 예를 들어 입력 데이터에 *1000을 취하면, 기울기는 1000배로 커지게 된다. 이런 경우 learning rate로 조절 해야하며, preprocessing(전처리)가 매우 중요하다는 것을 확인할 수 있다. 행렬과 벡터의 연산에도 위 개념들을 확장 가능하다. 그 과정에서 차원(dimension)과 전치(transpose)에 대한 주의가 필요하다.
Reference
CS231n 강의 노트 : https://cs231n.github.io/optimization-2/
'딥러닝 > Basic (CS231n)' 카테고리의 다른 글
| [CNN] Preprocessing (전처리), Weight init (가중치 초기화), Loss function (손실 함수) (0) | 2024.05.18 |
|---|---|
| [CNN] Neural Network(신경망), Neuron (뉴런), Activation function(활성화 함수) (0) | 2024.05.11 |
| [CNN] Optimization (최적화), Gradient(기울기 계산), Learning rate (0) | 2024.04.27 |
| [CNN] Linear classification (SVM, Softmax) (2) | 2024.04.20 |
| [CNN] Image Classification (이미지 분류), k-NN, Hyperparameter (1) | 2024.04.17 |