
Image Classification (이미지 분류)
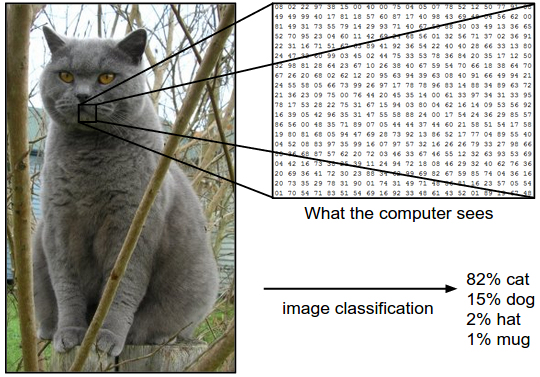
Image Classification 이란 이미지를 여러 레이블 집합 중 하나의 레이블(label)로 지정하는 작업이다. Object detection, Segmentation 도 Image Classification중 하나라고 할 수 있다. 위 이미지로 예시를 들자면, 단일 이미지를 {고양이, 개, 모자, 머그잔} 의 집합에서 각 레이블 별 확률을 구하게 되며, 이 중 가장 높은 확률인 "고양이"를 레이블로 예측한다.
이미지는 가로 248px, 세로 400px, RGB를 이루는 3 channel로 이루어져 있으며 297600개의 숫자로 구성되며, 각 숫자는 0~255 사이의 정수다. Image Classification이란 이 25만개의 숫자를 활용해 "고양이" 라는 단일 레이블로 변환(예측)하는 것이다. 다만 이미지를 인지하는 이 작업은 사람에게는 비교적 간단한 반면, 컴퓨터 비전 관점에선 여러 추가적인 문제가 존재한다.

- Viewpoint variation (관점 변화) : 동일한 객체도 여러 방향을 가질 수 있다.
- Scale variation (크기 변화) : 실제 세계 혹은 이미지 내에서 크기 변화가 존재한다.
- Defromation (변형) : 동일한 객체이나 극단적인 방법으로 변형될 수 있다.
(고양이 액체설..) - Occlusion (가려짐) : 가려질 수 있음. 때로는 객체의 아주 작은 부분(소수 픽셀만큼)만 보일 수 있다.
- Illumination conditions (조명 조건) : 조명의 차이는 픽셀 값(0~255)를 급격하게 변경시킨다.
- Background clutter (배경 혼잡) : 객체가 환경(배경)과 혼합되어 식별하기 어렵다.
- Intra-class variation (종내 변동) : 클래스(레이블)는 상대적으로 광범위할 수 있음. 예를 들어, 의자는 서로 다른 외관을 가지고 있다.
좋은 이미지 분류 모델은 위 7가지 변동과 같은 다양성에 대해 같은 클래스의 이미지 간에는 강인하면서, 서로 다른 클래스의 차이에 대해선 민감해야한다.

Data-driven approach (데이터 주도 접근 방식)
이미지의 클래스를 식별하는 것은 명확한 방식을 통해, 클래스를 직접적으로 설명하는 것이 아니다. 숫자 정렬 알고리즘과 같이 설명 가능한 명확한 방식이 존재하지 않는다. 이미지 분류 알고리즘은 컴퓨터에게 각 클래스 별로 많은 예제를 제공하고, 이 예제를 통해 시각적인 외형을 컴퓨터가 학습하는 방향으로 알고리즘을 구현하는 것이다. (Data-driven approach)
따라서 위 이미지와 같이 레이블이 지정된 dataset을 먼저 축적하는 것이 필요하다. 학습의 흐름(pipeline)은 아래와 같이 나눌 수 있다.
- Input (입력) : 입력은 N개의 이미지들의 집합으로 구성. 각 이미지는 M개의 서로 다른 클래스 중 하나로 레이블이 지정. 이 N개의 이미지 집합을 training set이라고 지칭.
- Learning (학습) : Training set을 사용하여 각 클래스가 어떻게 보이는지를 학습. 이 단계를 분류기를 훈련시키거나 모델을 학습시킨다고 표현. (training a classifier or learning a model)
- Evaluation (평가) : 모델의 성능을 평가하기 위해 동일힌 클래스 + 학습하지 않은 새로운 이미지 집합에 대해 레이블을 예측하도록 요청. 이후 이미지들의 실제 레이블을 모델이 예측한 것과 비교 및 성능을 수치화. ex) accuracy
Nearest Neighbor Classifier

Nearest Neighbor Classifier는 이미지 분류에서 처음으로 접근한 방식이다.CNN 방식이 아니며 현재 많이 쓰이는 방법은 아니나, 이미지 분류를 위한 기초적인 아이디어를 재공한다. Nearest neighbor classifier는 한 장의 test 이미지를 가져와 모든 training 이미지와 비교한 뒤, 가장 가까운 training 이미지의 레이블로 test 이미지를 예측한다.
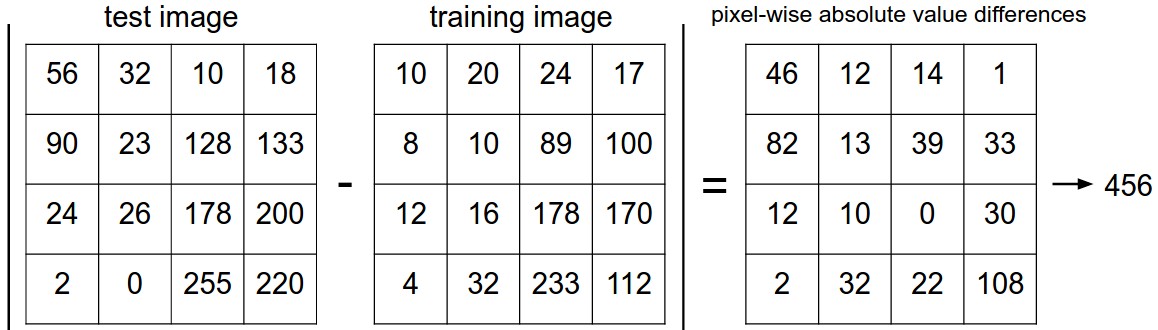
위 예시에선 가장 간단한 방법 중 하나인 L1 distance를 활용했으며, 약 10개 중 3개 정도 동일한 클래스로 예측한다.L1 dsitance란, 이미지를 픽셀 단위로 비교하고 모든 차이를 더하는 것이다. 각 이미지를 I1, I2로 나타내면 아래 수식으로 표현 가능하다.

두 이미지가 동일하면 결과는 0이 되며, 이미지가 매우 다르면 결과는 크게 나온다. 전체 test set의 L1 distance를 통한 정확도를 구하면 38.6%가 나오며, 10%의 랜덤 확률 보단 높으나 사람의 능력보단 크게 뒤쳐지는 수준이다. (추후 CNN을 통해 95% 수준의 정확도를 달성)
또 다른 거리 계산 방법에는 L2 distance가 있다. 이는 두 벡터 사이의 유클리드 거리를 계산하는 방식이다. L1 distance와 같이 픽셀 단위의 차이를 계산하지만, 이번에는 차이를 제곱하여 모두 더한 후 총합에 제곱근을 취한다. 다만, Code로 구현시에는 제곱근 연산이 생략될 수 있다. 그 이유는 제곱근이 단조 함수 (monotonic funtion)이며, 이는 크기는 조정하지만 순서는 동일하기 때문에 nearest neighbors는 동일하기 때문이다. 동일하게 전체 test set의 L2 distance를 통한 정확도를 구하면 35.4%가 나온다. >
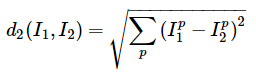
L1, L2 distance는 vector p-norm 중 가장 자주 사용되는 case 이며, 보통 L2 distance는 L1 distance보다 훨씬 더 엄격하다. 그 이유는 L2 distance는 하나의 값보다 중간 차이를 활용하기 때문이다. (직관적으로 받아들여지는 내용이 아니라 관련 내용을 좀 찾아보니, 아래 이미지와 같이 L2에서 제약 범위가 더 넓기 때문에 엄격하다라고 생각됨..)

k-Nearest Neighbor Classifier
가장 가까운 상위 k개의 이미지 중 가장 많이 나온 레이블로 테스트 이미지를 예측하는 방식이다. k=1은 Nearest Neighbor Classifier와 동일하며, k값이 커질수록 outlier에 강인해지는 smoothing effect가 커진다.
아래 이미지는 NN Classifier (k=1)과 5-NN Classifier 예시다. 각 색상이 클래스를 의미하며 L2 distance로 클래스의 경계를 의미한다. 또한 5-NN에서 흰색은 명확하게 클래스가 구분이 되지 않는 영역이다. Outlier가 NN에서는 중간 중간 잘못된 예측을 하는 일종의 섬 영역을 형성하게 된다. 이를 통해, 5-NN에서는 smoothing effect로 더 좋은 일반화(generalization)를 이끌어내는 것을 확인할 수 있다.

NN Clasifier의 장단점
- 장) 구현과 이해가 매우 간단 + 훈련하는 데 시간이 전혀 걸리지 않는다.
- 단) 모든 test set과 모든 training set의 비교가 필요하여 많은 계산량이 요구된다. 현재는 Approximate Nearest Neighbor (ANN) 알고리즘과 같이 NN Classifier의 계산 복잡성에 대한 연구는 진행 중이며, kdtree를 구축하거나 k-means 알고리즘을 실행하는 전처리/인덱싱 단계에 활용되기도 한다.

이미지 분류에서 성능이 좋지 않다. 위 이미지와 같이 pixel 기반의 L2 distance는 클래스의 특징을 표현하지 못한다.
t-SNE라고 불리는 시각화 기법을 통해 CIFAR-10 이미지를 배치한다면, 서로 가까이 보이는 이미지는 L2 distance가 가까운 것으로 간주할 수 있다. 이 중 서로 가까이 있는 이미지는 주로 색 분포나 배경 유형에 따라 달라진다. 예를 들어, 개는 하얀 배경에 있기 때문에 개와 개구리가 매우 가깝게 보일 수 있다. 클래스의 특징이 아닌 클래스와 관련이 없는 이미지의 특징 및 변화(배경과 같은)에 따라 서로 가까이 분포된다. 클래스의 특성을 얻기 위해선 "raw pixel"을 넘어서야 한다.

Hyperparameter
k-NN Classifier는 최적의 k가 필요하며, L1 norm, L2 norm 외에 수 많은 거리 함수가 존재한다. 이러한 모델의 구성하는 여러 정해지지 않은 선택 사항들을 Hyperparameter (하이퍼파라미터) 라고 하며, 모든 알고리즘에는 각각의 하이퍼파라미터가 존재한다. 문제는 어떤 하이퍼파라미터을 선택해야 하는지 명확하지 않다.
적정 Hyperparameter를 선택하기 위해 튜닝하는 과정을 필수적으로 수행. 이 과정에서 test set을 사용하지 않는 것이 중요하다. Test set은 모델의 최종 성능을 평가할 때만 사용하며, 그렇지 않으면 test set이 마치 train set이 되어 테스트시 잘 작동하는 것처럼 보이지만 새로운 데이터에 대해서는 성능이 나빠질 수 있다.
Train/Validation Set
하이퍼파라미터를 튜닝하는 올바른 접근 방법은 training set을 두 부분으로 나누는 방법이다. 전체 training set 중 일부를 validation set으로 분류하고, Validation set은 하이퍼파라미터를 조정하기 위해 test set을 대신하여 사용한다. 최적의 하이퍼파라미터를 결정하고 나면 모델의 최종 평가는 테스트 세트에서 수행한다.
Cross-validation (교차 검증)
데이터의 크기가 작을 경우, Cross-validation(교차 검증)을 사용하여 하이퍼파라미터 튜닝을 수행한다. 임의로 검증 세트로 선택하는 대신, 서로 다른 검증 세트를 반복하여 각 hyperparameter 값이 얼마나 잘 작동하는지 추정하는 방식이다. 예를 들어 5-fold cross-validation에선 training set을 5개의 동일한 크기의 폴드로 나누고, 이 중 4개를 훈련, 1개를 검증에 사용한다. (주로 3-fold, 5-fold, 10-fold를 사용) 서로 다른 fold를 검증에 사용하여 성능을 평가하고 (5-fold면 5회), 마지막으로 서로 다른 폴드 간의 성능을 평균을 구한다.

다만, 계>산량이 많기 때문에 일반적으로 교차 검증을 사용하기보다 단일 검증 분할을 선호한다. 보통 하이퍼파라미터의 수가 많은 경우 Validation set의 비율을 높이고 단일 검증. 반대의 경우 (Validation set의 비율이 낮은 경우) 교차 검증을 사용하는 것이 더 안전하다. Hyperparameter tuning에 대한 더욱 자세한 내용은 나중 강의에서 추가로 학습할 예정이다.
Reference
CS231n 강의 노트 : https://cs231n.github.io/classification/
'딥러닝 > Basic (CS231n)' 카테고리의 다른 글
| [CNN] Neural Network(신경망), Neuron (뉴런), Activation function(활성화 함수) (0) | 2024.05.11 |
|---|---|
| [CNN] Backpropagation(역전파), chain rule (0) | 2024.05.04 |
| [CNN] Optimization (최적화), Gradient(기울기 계산), Learning rate (0) | 2024.04.27 |
| [CNN] Linear classification (SVM, Softmax) (2) | 2024.04.20 |
| [CNN] CS231n 카테고리를 시작하며 (0) | 2024.04.14 |