
Parameter Update
기울기는 파라미터를 업데이트하는데 사용되며, 이를 수행하는데는 여러가지 방법이 있다.
Vanila (기본)
단순히 파라미터를 음의 기울기 방향으로 변경하는 것이다. 이 경우 loss를 최소화 하는 경우, 기울기의 반대로 내려가야한다. 기울기의 크기를 그대로 반영하는 것이 아닌 Learning rate를 곱합으로써 점진적으로 변경된다.
Momentum (모멘텀)
최적화 문제를 물리적인 관점에서 영감을 얻었으며, 기본방식보다 더 나은 수렴 속도를 가진다.Loss는 일종의 언덕이며, 초기화는 어느 입자의 초기 위치를 임의로 설정하는 것이다. U = mgh 라는 포텐셜 에너지를 입자는 가지고 있으며, 최적화는 이 입자가 굴러내려가는 과정으로 비유된다.
입자에 작용하는 힘은 포텐셜 에너지의 음의 기울기와 관련이 있다. (F=−∇U) 또한 F = ma이므로 이 관점에서입자의 가속도는 에너지의 음의 기울기에 비례한다. 이는 Vanila 방식은 위치를 구하는 방식이라면, Momentum은 속도를 구하는 방식이고 이 속도로 인해 위치가 변한다.
속도가 새로 계산될때마다 이전 속도에 mu(모멘텀)라는 하이퍼파라미터를 곱하여 구한다. (보통 0.9)이는 물리적으로 마찰 계수라고 생각 할 수 있다. mu가 없다면 입자는 언덕의 맨 아래에서 멈추지 않고 끊임없이 흐르게 된다. 경우에 따라 초기에는 mu가 작고 학습이 진행되면서 mu를 증가시킴으로 학습 방식을 개선시킬 수 있다.
Nesterov 모멘텀
이를 더 개선시킨 버전이 Nesterov 모멘텀이다. 이는 볼록 함수 형태의 loss에서 이론적으로 수렴을 보장하며, 실제로 성능이 약간 더 좋은 것으로 알려졌다. 기존의 방식은 현 위치 x에서 입자가 기존에 가지고 있던 모멘텀 관련 항과 현 위치의 기울기로 다음 위치를 계한다. Nesterov는 현 위치 x에 존재한 입지가 모멘텀에 의한 만큼 이동한 뒤, 이동한 위치의 기울기를 더하는 방식으로 이는 "오래된" x에서 기울기를 계산하는 것보단 합리적으로 볼 수 있다.

Newtons's method
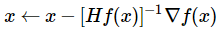
뉴턴의 법칙(수치해석학에서 실숫값 함수의 영점을 근사하는 방법)에 기반한 최적화 방식도 사용되기도 하다. Hf(x)는 Hessian 행렬로 loss function의 local curvature(곡률)을 의미하며,∇f(x)는 경사하강법과 같은 기울기 벡터이다. Hessian의 역행렬에 기울기를 곱함으로써 곡률이 작으면 급격히 움직이고, 곡률이 크면 더 조심스럽게 움직이게된다. 이 방식의 중요한 점은 모멘텀 mu와 같이 하이퍼파라미터가 불필요하다는 점이다.
다만, 현실적으로 실용적인 방법은 아님. 이유는 Hessian 행렬의 계산은 연산량이 매우 크기 때문이다. 또한 L-BFGS라는 역 Hessian 행렬의 근사치를 이용하는 방법이 개발되었다. 그러나 전체 training set에 대한 계산이 필요한 단점이 있으며 , 모멘텀에 기반을 둔 SGD가 훨씬 간단하고 확장성이 넓다.
Annealing the learning rate
Learning rate을 점차 줄이는 것은 신경망을 훈련시킬 때 보통 도움이 된다. 높은 learning rate은 파리미터가 변동하는 에너지가 너무 커 불규칙하게 튀어다니며, 깊고 좁은 그리고 값이 굉장히 작은 loss의 최적지점에 도달하지 않은 것으로 볼 수 있다. 이에 learning rate를 줄이긴 줄이나, 어느정도의 속도로 어느 만큼 줄이는것이 좋을지에 대한 고민이 필요하다.
- Step decay (단계적인 감소):일정한 주기마다 조건을 만족하면 일정 크기의 learning rate를 감소시킨다. 모델의 유형이나 해결하고자하는 문제에 따라 그 크기와 횟수는 달라진다. 사용되는 방식 중 하나는 val error가 일정 주기가 지나도 개선되지 않을 때마다 특정 값만큼 learning rate를 줄인다.
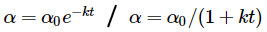
- Exponential decay (지수 감소)or1/t decay (1/t 감소) : t번 반복(epoch) 할 때마다 일정 비율로 감소시킨다.Step decay가 직관적으로 해석 및 이해가 쉽기에 조금 더 선호되는 방식이다.연산량에 여유가 있다면 더 천천히 learning rate을 줄이고 오래 학습하는것이 근본적으로 좋은 방법이다
Adaptive learning rate (적응형 학습률)
위에서 다룬 방법을 모든 파라미터를 동등하게 조절하는 방법이다.이후 Learning rate 및 각 파라미터를adaptive하게 조정하고 더 나아가 개별적으로 조정할 수 있는 방법을 개발되었다. 이러한 방식은 부가적인 하이퍼파라미터를 필요로 할 수 있지만, 더 넓은 범위에서 좋은 결과를 보인다는 결과가 있다.
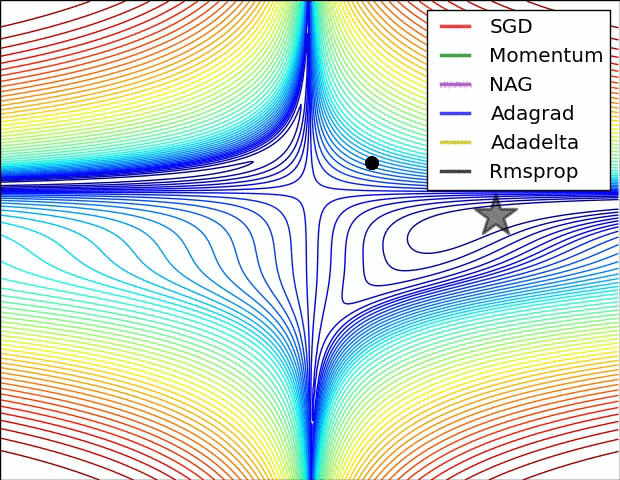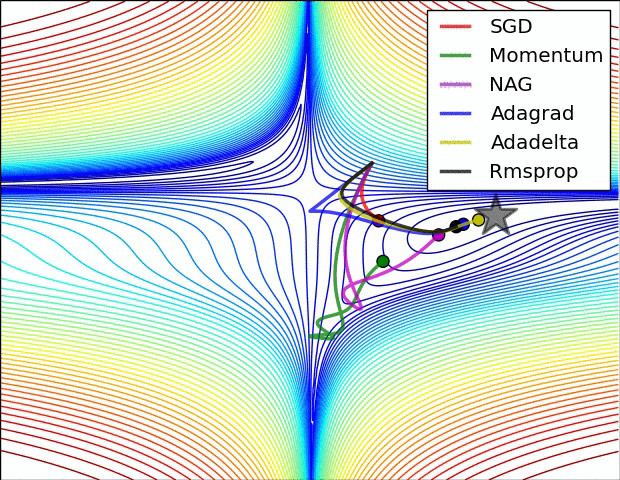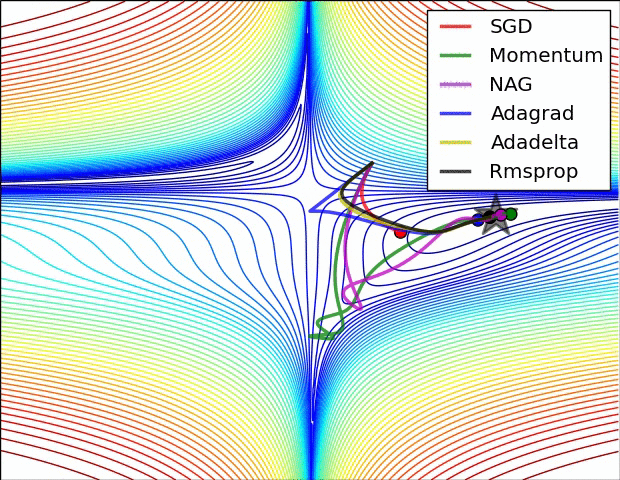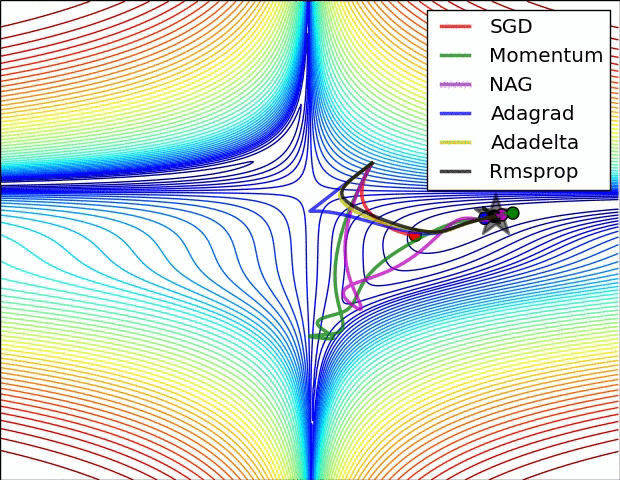
Adagard
cache += dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps) # eps는 0으로 나뉘는 것을 방지변수 cache의 크기는 기울기의 크기와 같다고 볼 수 있다. 그리고 파라미터 기울기의 제곱합을 추적한다. 이는 파라미터를 elemnet-wise하게 normalize 하는데 사용된다. 즉, 큰 기울기를 가지는 w는 learning rate가 낮아지고, 작은 기울기를 가지는 w는 learning rate가 증가하는 효과를 가져온다.
제곱의 합의 제곱근을 취하는 방식은 언뜻보면 불필요해보이지만 결과론적으로 더 좋은 효과를 유도한다. Adagard의 단점으론, 학습을 매우 빠르게 진행하고 일찍 멈추려는 경향을 가지게 한다.
RMSprop
cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)
RMSProp는 Adagrad 방법을 매우 간단하게 조정하여 급격한 학습 현상을 줄이려고 시도한다. 이는 제곱된 기울기에 이동 평균을 사용함으로 구현된다. decay_rate는 하이퍼파라미터이고 일반적으로 [0.9, 0.99, 0.999] 이 사용된다. "x+="는 동일하며cache 변수는 각 가중치의 기울기 크기에 따라 변화하는 것은 동일하나 크기의 일부만 반영되어, monotonically(단조롭게)하게 감소되진 않는다. (Adagard가 급격하게 변화되는 원인)
Adam
m = beta1*m + (1-beta1)*dx
v = beta2*v + (1-beta2)*(dx**2)
x += - learning_rate * m / (np.sqrt(v) + eps)
RMSProp에 모멘텀을 추가한 것이다. "x +=" 는 여전히 동일하나 기울기를 기존 dx 대신 "smooth"해진 m을 사용한다.추가된 beta1, beta2는 하이퍼파라미터로 beta1 = 0.9, beta2 = 0.999 정도를 논문에선 권장한다.
하이퍼파라미터 최적화
신경망을 훈련할 때, 수 많은 하이퍼파라미터를 설정해줘야한다. (learning rate, decay schedule, regularization 등) 이 중 일부는 epoch 마다 민감하고 조절해야하기도 하고, 일부는 민감하지 않아 특정 값으로 fix 해도 된다. 아래는 이를 수행 하는 tip 과 trick을 소개한다.
Implementation (구현)
신경망이 클 수록훈련에 많은 시간이 소요되므로 하이퍼파라미터 서칭에 많은 날/주가 소요될 수 있다. 이를 염두하여 코드를 작성해야하며, worker를 구현해야한다. 이는계속해서 무작위 하이퍼파라미터를 샘플링하고 최적화를 수행한다. 또한매 epoch마다 성능을 추적하고 (loss, time 등의 학습 관련 통계치에 대해) 모델 checkpoint를 파일로 저장하여 이력 확인에도 용이하다.
이러한 정보를 Master 라 하는 프로그램을 구현하여, worker의 시작과 종료를 판단한다. worker가 작성한 checkpoint를 검사하고 관련 통계를 plot하는 등의 작업을 수행할 필요가 있다.
Cross-validation(교차 검증)을 위한 단일 fold를 사용
여러 개의 fold를 사용하는 것보다 합리적인 크기의 단일validation set을 사용하는 것이 코드를 간소화 해준다. 파라미터를 "cross-validated" 했다고 하나, 대부분 val set으로만 검증한 경우가 대부분이다.
하이퍼파라미터의 범위
로그 스케일로 하이퍼파라미터를 서칭한다. (ex : 1e-1,1e-2,1e-3,1e-4, ....) 이러한 범위 지정은 learning rate, regularization strength 와 같이 "곱셈"을 통해 학습에 영향을 주는 하이퍼파라미터인 경우에 한 한다. 그 이유는 10 일 때 0.01을 더하는 것은 의미가 없으나, 0.001에 0.01을 더하는 것은 의미가 있기 때문이다. 즉, 덧셈, 뺄셈을 검증하는 범위보다,곱셈, 나눗셈을 검증하는 범위를 고려하는 것이 더 합리적이다. 이 관점에서 절대적인 숫자가 의미가 있는 파라미터(ex: dropout의 p)는 실수 범위의 스케일로 서칭한다.
규칙적인 서칭이 아닌 무작위 서칭
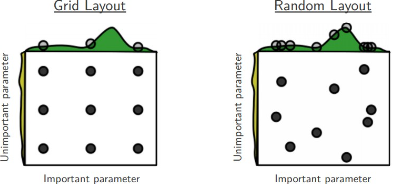
Grid 서칭 (규칙적인 형태) 대신Random 서치를 수행하면 중요한 하이퍼파라미터의 더 좋은 값들을 발견한다.이는 몇몇 하이퍼파라미터는 특정 값에서 훨씬 성능이 좋을 수 있기 때문이다. 즉, 모든 하이퍼파리미터를 동일한 범주내의 집합으로 서칭하기 보단, 다양한 값이 서칭될 수 있게 하는 것이 유리하다.
최상의 결과를 보인 설정이 경계에 위치한 경우를 주의
예를 들어, Lr = 10 ** uniform(-6, 1)을 서칭한다고 가정하자. 이 중 10 ** -6 이 최고의 결과라면 검색한 구간 넘어에 최적의 하이퍼파라미터를 놓칠 수 있다.
광범위에서 시작하여 세세한 범위까지 단계적으로 진행
예시로10 ** [-6, 1]와 같이 log 스케일에서 광범위하게 검색한 후, 확인된 최적의 하이퍼파라미터를 기준으로 촘촘한 간격의 서칭을 추가적으로 진행한다. 또한 광범위하면 아예 훈련이 불가능한 경우도 존재하기에, 1회의 epoch에서만 첫번째 서칭을 진행한다. 이후 적절한 범위로 두번째 서칭을 진행할때는 5epoch 정도, 이를 반복하며 범위를 좁히고 epoch을 늘리는 것이 좋다.
Bayesian Hyperparameter Optimization
하이퍼파라미터을 더 효율적으로 탐색하기 위한 알고리즘을 개발하는 연구 분야다. 이는 exploration(탐색) - exploitation (활용)의 trade-off를 적절하게 설정하는 것으로,Spearmint, SMAC,Hyperopt 등이 유명하다.하지만 서칭 범위를 좁혀가며 직접 하이퍼파라미터를 찾는 것 이상의 성능을 보이진 못한다.
Evaluation (평가)
Ensemble (양상블)이란여러 독립적인 모델을 훈련하고 테스트 시간에 그들의 예측을 평균하는 것이다.평가 단계에서신경망 성능을 개선하는 방법 중 하나로 모델의 다양성이 증가할수록 그 성능은 향상된다. 아래는 앙상블을 구현하는 여러가지 방법이다.
- Same model, different initializations. (같은 모델, 다른 초기화)교차 검증을 사용하여 최적의 하이퍼파라미터를 결정한 다음,서로 다른 초기화를 사용해 여러 모델을 훈련한다.
- Top models discovered during cross-validation. (상위 모델을 발굴)교차 검증을 사용하여 최적의 하이퍼파라미터 순위를 구하고 그 중 상위 일부 만 앙상블로 형성하여 훈련한다. 최적이 아닌 모델이 포함되는 단점이 있으나, 교차 검증에 사용한 학습을 그대로 사용할 수 있어 시간적으로 좋다.
- Different checkpoints of a single model. (단일 모델의 서로 다른 checkpoint) 단일 네트워크의 서로 다른 체크포인트(예: 각 에폭 이후)를 사용하여 앙상블을 형성한다.이는 단일 네트워크 자체가 굉장히 용량이 큰 무거운 모델에 해당한다. 여러 개의 네트워크를 구성하는 것에 비하면 굉장히 가벼운 방법에 속한다.
- Running average of parameters during training. (훈련 중 모든 가중치의 평균을 구함)네트워크를 여러 반복 학습을 평균화하며, 마지막 몇 단계의 "부드러운" 버전의 가중치는 더 나은 val error를 얻는다. 이는 곧 loss가 그릇 모양이라 할때, 가중치는 최적점 주변을 맴돌고, 마지막 step보다 평균이 더 가깝다는 가정한다.마지막으로, 앙상블 모델의 단점은 테스트 시간이 훨씬 길어진다는 것이다.
Reference
CS231n 강의 노트 :https://cs231n.github.io/neural-networks-3/
'딥러닝 > Basic (CS231n)' 카테고리의 다른 글
| [CNN] Convolutional Neural Networks (CNN) (2) | 2024.06.15 |
|---|---|
| [CNN] Softmax classifer vs Neural Network Case Study (2) | 2024.06.08 |
| [CNN] Gradient check, 모델 학습 지표 (0) | 2024.05.25 |
| [CNN] Preprocessing (전처리), Weight init (가중치 초기화), Loss function (손실 함수) (0) | 2024.05.18 |
| [CNN] Neural Network(신경망), Neuron (뉴런), Activation function(활성화 함수) (0) | 2024.05.11 |